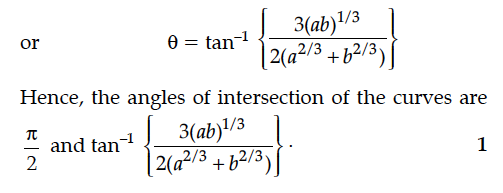Question

Consider $f\colon R^{+}\to[-9,\infty)$ given by f(x) = 5x² + 6x – 9.Prove that f is invertible with f⁻¹(y) = $\left({\frac{{\sqrt{54+5y}}-3}{5}}\right)$ [where, R⁺ is the set of all nonnegative real numbers.]

Find the particular solution of the differential equation $\left(1+x^{2}\right){\frac{d y}{d x}}=\left(e^{{\mathrm{mtan}^{\perp}x}}-y\right)$ given that y = 1 when x = 0.

Prove that the curves x = y² and xy = k cut at right angles if 8k² = 1.

Solve the differential equation : ${\frac{d y}{d x}}-3y\cot x=\sin2x\operatorname{given}y=2,{\mathrm{~when~}}x={\frac{\pi}{2}}.$

Find the equation of the normal at a point on the curve x² = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.

Find the equation of the tangent to the curve $\begin{array}{r c l}{y}&{=}&{{\sqrt{3x-2}}}\end{array}$ which is parallel to the line 4x – 2y + 5 = 0.

Find the equation of the tangent line to the curve y =x² -2x + 7 which is (i) parallel to the line 2x-y +9 =0 (ii) perpendicular to the line 5y - 15x = 13.