Question

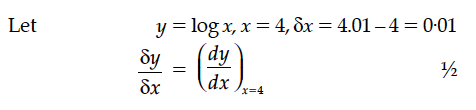
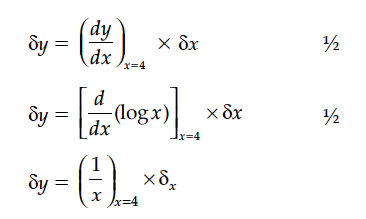
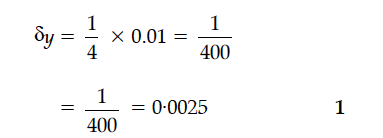
If x changes from 4 to 4·01, then find the approximate change in log x.

If E and F be two events such that P(E) = 1/3, P(F) = 1/4, find P(E U F) if E and F are independent events.

If A and B are two independent events, prove that A’ and B are also independent.

If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’)

Find the general solution of the differential equation ${\frac{d y}{d x}}+{\frac{2}{x}}y=x$

The radius r of a right circular cylinder is increasing at the rate of 5 cm/min and its height h, is decreasing at the rate of 4 cm/min. When r= 8 cm and h = 6 cm, find the rate of change of the volume of cylinder.

The position vectors of points A, B and C are $λ\stackrel{\wedge}{i}+3\stackrel{\wedge}{j}$,$12\stackrel{\wedge}{i}+μ\stackrel{\wedge}{j}$ and $11\stackrel{\wedge}{i}-3\stackrel{\wedge}{j}$ respectively. If C divides the line segment joining A and B in the ratio 3 : 1, find the values of λ and μ.