Find the equation of the tangent to the curve y=√3x−2 which is parallel to the line 4x – 2y + 5 = 0.

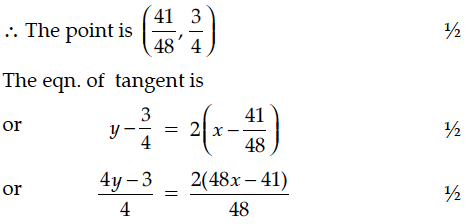
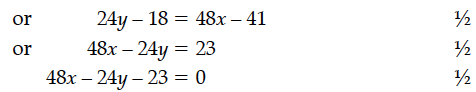
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Find the equation of tangent to the curve y = cos (x + y), -2π ≤ x ≤ 0, that is parallel to the line x + 2y = 0.
Find the equations of the normal to the curve y = x³+ 2x + 6, which are parallel to line x + 14y + 4 = 0.
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.
Find the equation of tangent to the curve y=x−7x2−5x+6 at the point, where it cuts the x-axis.
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the particular solution of the differential equation (1+x2)dydx=(emtan⊥x−y) given that y = 1 when x = 0.
Find the particular solution of the differential equation (1+y2)+(x−etan−1y) dydx=0, given that y = 0 when x = 1.
LetA = {x ∈ Z:0≤ x ≤12}. Show that R={(a,b):a,b ∈ A, |a-b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also write the equivalence class [2].
Find the equation of tangent and normal to the curve x = 1 – cos θ, y = θ – sin θ at θ = π4.
Consider the experiment of tossing a coin. If the coin shows head, toss is done again, but if it shows tail, then throw a die. Find the conditional probability of the events that ‘the die shows a number greater than 4’, given that ‘there is atleast one tail’.
Find the equation of the tangent line to the curve y =x² -2x + 7 which is
(i) parallel to the line 2x-y +9 =0
(ii) perpendicular to the line 5y - 15x = 13.
Find the equations of tangents to the curve 3x² – y² = 8, which passes through the point (43,0).
