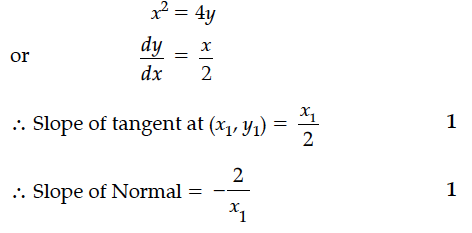
Find the equations of the normal to the curve y = x³+ 2x + 6, which are parallel to line x + 14y + 4 = 0.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the points on the curve y = x³ – 3x² – 9x + 7 at which the tangent to the curve is parallel to the x-axis.
Solve the following differential equation. (1 + y²) (1 + log |x|) dx + x dy = 0
Find the point on the curve y = x³ – 11x + 5 at which the equation of tangent is y = x – 11.
Show that the relation R on the set Z of all integers defined by (x, y) ∈ is divisible by 3 is an equivalence relation.