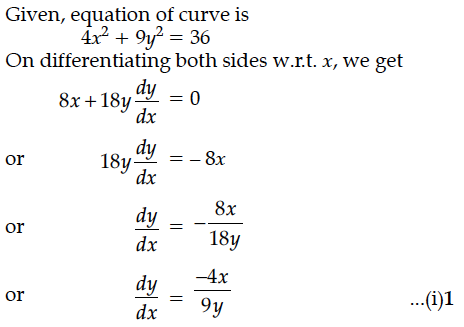
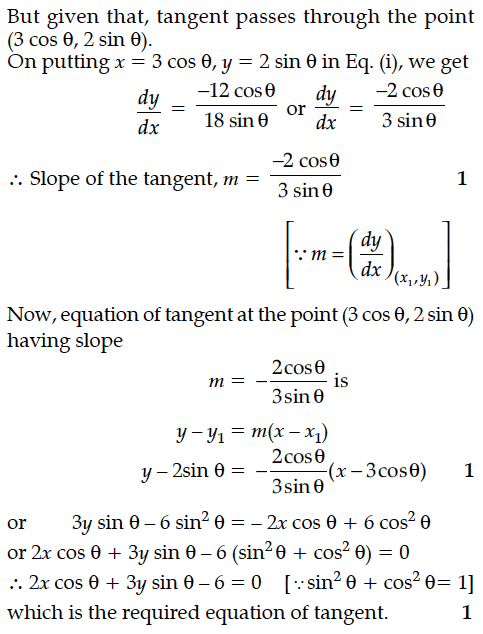
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Find the slope of tangent to the curve y = 3x² – 6 at the point on it whose x-coordinate is 2.
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the equations of tangents to the curve y = (x²– 1) (x – 2) at the points, where the curve cuts the X-axis.
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
If Z is the set of all integers and R is the relation on Z defined as R = {(a, b) : a, b ∈ Z and a – b is divisible by 5}. Prove that R is an equivalence relation.
Let f : W → W be defined as show that f is invertible. Find the inverse of f,where W is the set of all whole numbers.
A speaks truth in 60% of the cases, while B in 90% of cases. In what percent of cases are they likely to contradict each other in stating the same fact ? In the cases of contradiction do you think, the statement of B will carry more weight as he speaks truth in more number of cases than A ?
If the function f : R → R is given by f(x) = and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Is f⁻¹ = g?
In a school, there are 1,000 students, out of which 380 are girls. Out of 380 girls, 10% of the girls scored highest in GS. What is the probability that a student chosen randomly scored highest in GS given that the chosen student is a girl ?