Find the equation of the normal at the point (am², am³) for the curve ay² = x³.
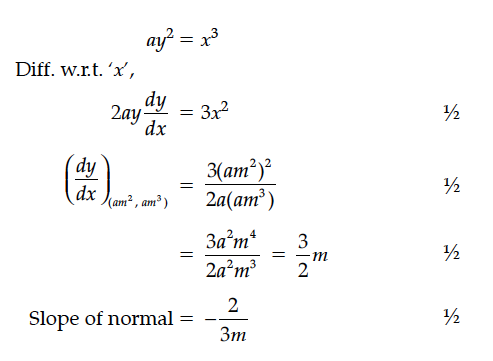
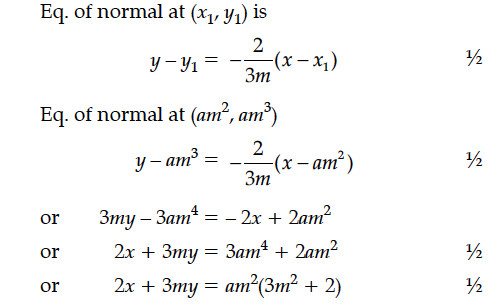
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the equations of the normal to the curve y = x³+ 2x + 6, which are parallel to line x + 14y + 4 = 0.
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Find the particular solution of the differential equation : x ≠ 0. Given that y = 0, when
Form the differential equation representing family of ellipses having foci on X-axis and centre at the origin.
Show that f : N → N, given by f(x) = |``x+1, if x is odd x- 1, if x is even is both one-one and onto.``|
If the radius of sphere is measured as 9 cm with an error of 0.03 cm, then find the approximate error in calculating its surface area.
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls ? Given that :
(i) the youngest is a girl.
(ii) atleast one is a girl.
