Find the equation of the normal at a point on the curve x² = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.
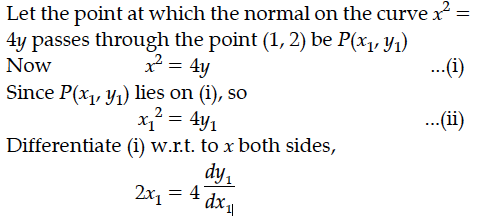

Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Find the equations of tangents to the curve 3x² – y² = 8, which passes through the point
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
The equation of tangent at (2, 3) on the curve y² = ax³ + b is y = 4x – 5. Find the values of a and b.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the equations of the normal to the curve y = x³+ 2x + 6, which are parallel to line x + 14y + 4 = 0.
Find the equations of tangents to the curve y = (x²– 1) (x – 2) at the points, where the curve cuts the X-axis.
Find the equation of tangent and normal to the curve x = 1 – cos θ, y = θ – sin θ at θ =
LetA = {x ∈ Z:0≤ x ≤12}. Show that R={(a,b):a,b ∈ A, |a-b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also write the equivalence class [2].
Show that the function f:R → R defined by f(x) = is neither one-one nor onto. Also,
if g:R → R is defined as g(x) = 2x – 1, find fog(x).
Find the equation of the tangent to the curve which is parallel to the line 4x – 2y + 5 = 0.
Let N denote the set of all natural numbers and R be the relation on N × N defined by (a, b) R (c, d) if ad(b + c) = bc(a + d). Show that R is an equivalence relation.
Find the equations of tangents to the curve 3x² – y² = 8, which passes through the point
Find the equation of the tangent line to the curve y =x² -2x + 7 which is
(i) parallel to the line 2x-y +9 =0
(ii) perpendicular to the line 5y - 15x = 13.
