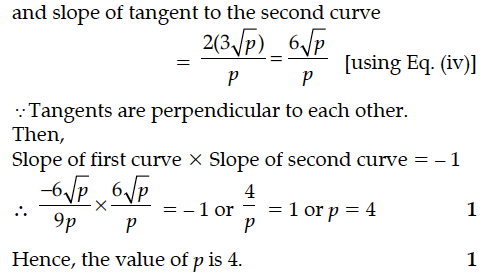
Find the slope of tangent to the curve y = 3x² – 6 at the point on it whose x-coordinate is 2.
Find the points on the curve x² + y² – 2x – 3 = 0 at which tangent is parallel to x-axis.
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the angle of intersection of the curves x² + y² = 4 and (x – 2)² + y²= 4, at the point in the first quadrant.
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Show that the normal at any point θ to the curve x = a cos θ + aθ sin θ, y = a sin θ – aθ cos θ is at a constant distance from the origin.
Let N denote the set of all natural numbers and R be the relation on N × N defined by (a, b) R (c, d) if ad(b + c) = bc(a + d). Show that R is an equivalence relation.
Find the angle of intersection of the curves y² = 4ax and x²= 4by.
Show that the relation R in the Set A = {1, 2, 3, 4,5} given by R = {(a, b) : |a – b| is divisible by 2} is an equivalence relation. Write all the equivalence classes of R.
Find the equation of tangent and normal to the curve x = 1 – cos θ, y = θ – sin θ at θ =
LetA = {x ∈ Z:0≤ x ≤12}. Show that R={(a,b):a,b ∈ A, |a-b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also write the equivalence class [2].
In a hockey match, both teams A and B scored same number of goals up to the end of the game, so to decide the winner, the referee asked both the captains to throw a die alternately and decided that the team, whose captain gets a six first, will be declared the winner. If the captain of team A was asked to start, find their respective probabilities of winning the match and state whether the decision of the referee was fair or not.