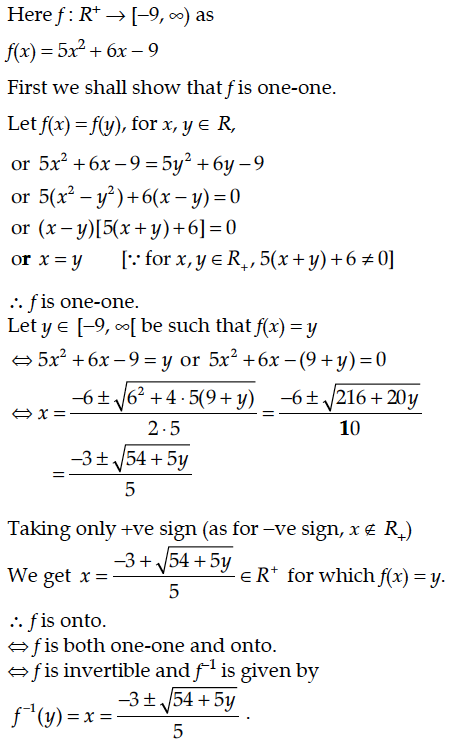
Consider f : given by f(x) = x² + 4 Show that f is invertible with the inverse of f given by = , where is the set of all nonnegative real numbers.
If the function f : R → R be given by f(x) = x² + 2 and g : R → R be given by g(x) = find fog and gof and hence find fog(2) and gof(– 3).
Prove that the function f : [0, ∞) → R given by f(x) = 9x² + 6x – 5 is not invertible. Modify the Codomain of the function f to make it invertible, and hence find f⁻¹.
Let A = R – {2}, B = R – {1}. If f : A → B is a function defined by show that f is one-one and onto. Hence find
Let f : R → R be defined by f(x) = 3x² – 5 and g : R → R be defined by g(x) = find gof(x) .
If the function f : R → R is given by f(x) = x² + 3x + 1 and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Show that the function f : R {x ∈ R – 1 < x < 1} defined by f(x) = x ∈ R is one-one and onto function. Hence find f⁻¹(x).
Show that the function f:R → R defined by f(x) = is neither one-one nor onto. Also,
if g:R → R is defined as g(x) = 2x – 1, find fog(x).
Find the particular solution of the differential equation given that y = 1 when x = 0.
Consider the experiment of tossing a coin. If the coin shows head, toss is done again, but if it shows tail, then throw a die. Find the conditional probability of the events that ‘the die shows a number greater than 4’, given that ‘there is atleast one tail’.
Find the equations of tangents to the curve 3x² – y² = 8, which passes through the point
Solve the differential equation x cos x + sin x, given that y = 1 when