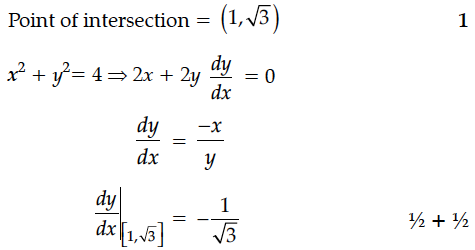
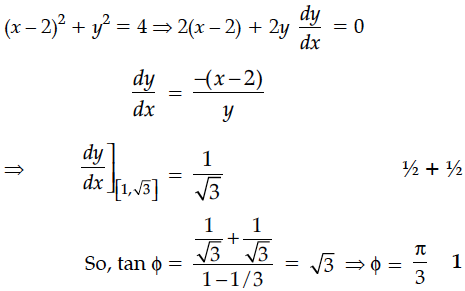
Find the points on the curve x² + y² – 2x – 3 = 0 at which tangent is parallel to x-axis.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the value of p for which the curves x² = 9p(9 – y) and x² = p(y + 1) cut each other at right angles.
Find the slope of tangent to the curve y = 3x² – 6 at the point on it whose x-coordinate is 2.
Find the equations of tangents to the curve y = (x²– 1) (x – 2) at the points, where the curve cuts the X-axis.
Find the equation(s) of the tangent(s) to the curve y = (x³ – 1) (x – 2) points where the curve intersects the x-axis.
Show that the relation R on the set Z of all integers defined by (x, y) ∈ is divisible by 3 is an equivalence relation.
Show that the equation of tangent to the parabola y² = 4ax at (x₁, y₁) is yy₁ = 2a(x + x₁).
If the function f : R → R be given by f(x) = x² + 2 and g : R → R be given by g(x) = find fog and gof and hence find fog(2) and gof(– 3).
P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree
in stating the same fact ?
Find the particular solution of the differential equation : 4x cosec x, (x ≠ 0), given, that y = 0,when
Find the equation of tangent to curves x = sin 3t, y = cos 2t at