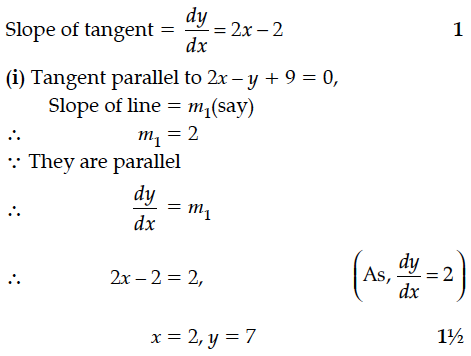
Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
Find the equations of the normal to the curve y = x³+ 2x + 6, which are parallel to line x + 14y + 4 = 0.
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Find the equation of tangent to the curve y = cos (x + y), -2π ≤ x ≤ 0, that is parallel to the line x + 2y = 0.
Find the equation(s) of the tangent(s) to the curve y = (x³ – 1) (x – 2) points where the curve intersects the x-axis.
Find the equations of tangents to the curve y = (x²– 1) (x – 2) at the points, where the curve cuts the X-axis.
Consider given by f(x) = Show that f is bijective. Find the inverse of f and hence find f⁻¹(0) and x such that f⁻¹(x) = 2.
Show that the relation R in the Set A = {1, 2, 3, 4,5} given by R = {(a, b) : |a – b| is divisible by 2} is an equivalence relation. Write all the equivalence classes of R.
Find the angle of intersection of the curves y² = 4ax and x²= 4by.
Let N denote the set of all natural numbers and R be the relation on N × N defined by (a, b) R (c, d) if ad(b + c) = bc(a + d). Show that R is an equivalence relation.
Find the equation of the normal at a point on the curve x² = 4y which passes through the point (1, 2). Also find the equation of the corresponding tangent.
Find the equation of the tangent line to the curve y =x² -2x + 7 which is
(i) parallel to the line 2x-y +9 =0
(ii) perpendicular to the line 5y - 15x = 13.
If A and B are two independent events such that P(A' ∩ B)= 2/15 and P(A ∩ B')= 1/6, then find P(A) and P(B).