Write the equation of tangent drawn to the curve y = sin x at the point (0, 0).
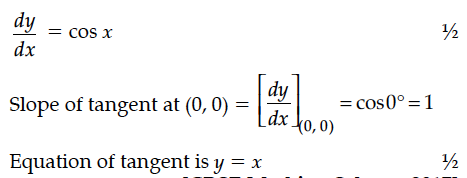
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Find the slope of tangent to the curve y = 3x² – 6 at the point on it whose x-coordinate is 2.
Find the scalar components of the vector with initial point A(2,1) and terminal point B (– 5, 7).
For a 2 x 2 matrix, A = [] whose elements are given by = write the value of
State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive.
