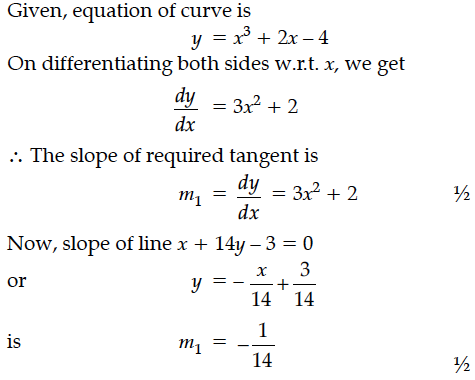
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
Find the equations of the normal to the curve y = x³+ 2x + 6, which are parallel to line x + 14y + 4 = 0.
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Find the equation of tangent to the curve y = cos (x + y), -2π ≤ x ≤ 0, that is parallel to the line x + 2y = 0.
Find the equations of tangents to the curve y = (x²– 1) (x – 2) at the points, where the curve cuts the X-axis.
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Show that the relation R on the set Z of all integers defined by (x, y) ∈ is divisible by 3 is an equivalence relation.
A problem in mathematics is given to 4 students A, B, C, D. Their chances of solving the problem, respectively, are 1/3, 1/4, 1/5 and 2/3. What is the probability that
(i) the problem will be solved ?
(ii) at most one of them solve the problem ?
Let f, g : R → R be two functions defined as f (x) = |x| + x and g (x) = |x| – x for all x ∈ R.Then find fog and gof.
A and B throw a pair of dice alternately. A wins the game if he gets a total of 9 and B wins if he gets a total of 7. If A starts the game, find the probability of winning the game by B.
Find the particular solution of the differential equation given that y = 1, when x = 0.