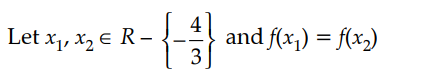
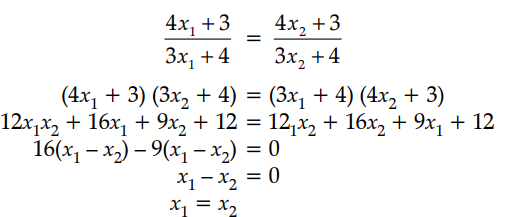
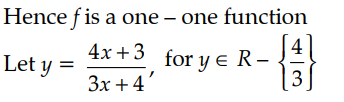
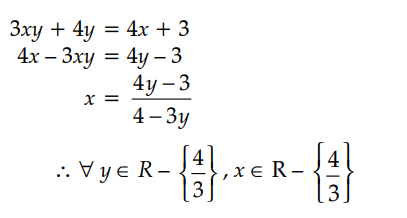
If the function f : R → R be given by f(x) = x² + 2 and g : R → R be given by g(x) = find fog and gof and hence find fog(2) and gof(– 3).
If the function f : R → R is given by f(x) = and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Is f⁻¹ = g?
Let A = R – {3}, B = R – {1}. Let f : A → B be defined by f(x) = Show that f is bijective. Also, find
(i) x, if = 4
(ii)
Show that the function f : R {x ∈ R – 1 < x < 1} defined by f(x) = x ∈ R is one-one and onto function. Hence find f⁻¹(x).
Let f : W → W be defined as show that f is invertible. Find the inverse of f,where W is the set of all whole numbers.
If the function f : R → R be defined by f(x) = 2x – 3 and g : R → R by g(x) = x³ + 5, then find fog and show that fog is invertible. Also, find (fog)⁻¹, hence find (fog)⁻¹(9).
Find the equation of the tangent line to the curve y =x² -2x + 7 which is
(i) parallel to the line 2x-y +9 =0
(ii) perpendicular to the line 5y - 15x = 13.
Show that the function f:R → R defined by f(x) = is neither one-one nor onto. Also,
if g:R → R is defined as g(x) = 2x – 1, find fog(x).
In a hockey match, both teams A and B scored same number of goals up to the end of the game, so to decide the winner, the referee asked both the captains to throw a die alternately and decided that the team, whose captain gets a six first, will be declared the winner. If the captain of team A was asked to start, find their respective probabilities of winning the match and state whether the decision of the referee was fair or not.
If A and B are two independent events such that P(A' ∩ B)= 2/15 and P(A ∩ B')= 1/6, then find P(A) and P(B).
Show that the function f : R {x ∈ R – 1 < x < 1} defined by f(x) = x ∈ R is one-one and onto function. Hence find f⁻¹(x).
Show that the relation R in the Set A = {1, 2, 3, 4,5} given by R = {(a, b) : |a – b| is divisible by 2} is an equivalence relation. Write all the equivalence classes of R.
Find the equation of the tangent to the curve which is parallel to the line 4x – 2y + 5 = 0.