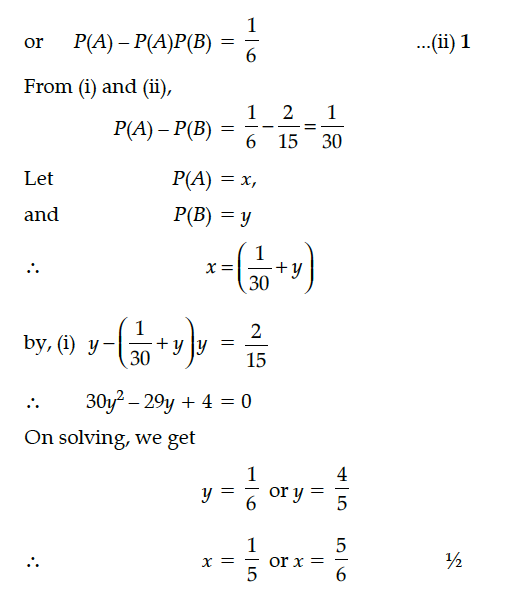
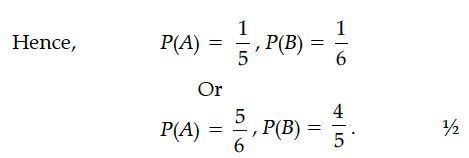
If A and B are two events such that P(A) = 0.4, P(B) = 0.8 and P(B/A) = 0.6, then find P(A/B).
If E and F be two events such that P(E) = 1/3, P(F) = 1/4, find P(E U F) if E and F are independent events.
If E and F are two events such that P(E) = 1/4, P(F) = 1/2 and P(E ∩ F) = 1/8, find
(i) P(E or F)
(ii) P(not E and not F).
Show that the function f:R → R defined by f(x) = is neither one-one nor onto. Also,
if g:R → R is defined as g(x) = 2x – 1, find fog(x).
Solve the differential equation x cos x + sin x, given that y = 1 when
Find the equations of tangents to the curve 3x² – y² = 8, which passes through the point
Find the particular solution of the differential equation (x – sin y) dy + (tan y) dx = 0, given that y = 0 when x = 0.
Find the value of p for which the curves x² = 9p(9 – y) and x² = p(y + 1) cut each other at right angles.
Show that the normal at any point θ to the curve x = a cos θ + aθ sin θ, y = a sin θ – aθ cos θ is at a constant distance from the origin.