Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
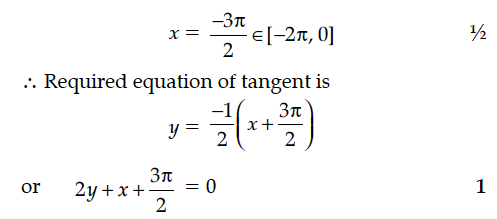
Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.
Find the equations of the normal to the curve y = x³+ 2x + 6, which are parallel to line x + 14y + 4 = 0.
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
Find the equations of tangents to the curve y = (x²– 1) (x – 2) at the points, where the curve cuts the X-axis.
Check whether the relation R in the set R of real numbers, defined by R = {(a, b) : 1 + ab > 0}, is reflexive, symmetric or transitive.
Let f, g : R → R be two functions defined as f (x) = |x| + x and g (x) = |x| – x for all x ∈ R.Then find fog and gof.
Show that the equation of tangent to the parabola y² = 4ax at (x₁, y₁) is yy₁ = 2a(x + x₁).
Find the general solution of the following differential equation :
Form the differential equation representing family of ellipses having foci on X-axis and centre at the origin.