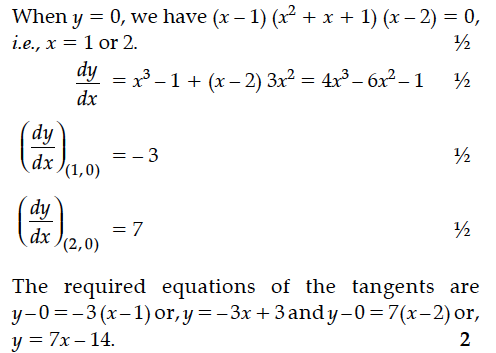
Find the equations of tangents to the curve y = (x²– 1) (x – 2) at the points, where the curve cuts the X-axis.
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the slope of tangent to the curve y = 3x² – 6 at the point on it whose x-coordinate is 2.
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Two farmers X and Y cultivate only three varieties of rice namely Basmati, Permal and Naura. The sale in rupees of these varieties of rice by both the farmers in the months of September and October are given by the following matrices A and B.
If the function f : R → R be defined by f(x) = 2x – 3 and g : R → R by g(x) = x³ + 5, then find fog and show that fog is invertible. Also, find (fog)⁻¹, hence find (fog)⁻¹(9).
Form the differential equation of the family of circles in the second quadrant and touching the co-ordinate axes.
Show that the relation S in the set R of real numbers defined as S = {(a, b) : a, b ∈ R and a ≤ b³} is neither reflexive nor symmetric nor transitive.
If the function f : R → R is given by f(x) = x² + 3x + 1 and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Find the particular solution of the following differential equation :
y = 0, when x = 2.