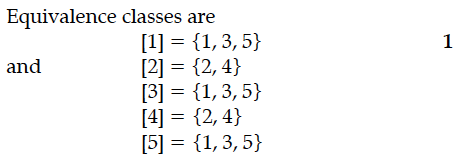
Let R be the equivalence relation in the set A = {0, 1, 2, 3, 4, 5} given by R = {(a, b) : 2 divides (a –b)}. Write the equivalence class [0].
Show that the relation S in the set R of real numbers defined as S = {(a, b) : a, b ∈ R and a ≤ b³} is neither reflexive nor symmetric nor transitive.
Show that the relation R in the set N × N defined by (a, b) R (c, d) if a² + d² = b² + c² is an equivalence relation.
Show that the relation R on the set Z of all integers defined by (x, y) ∈ is divisible by 3 is an equivalence relation.
Check whether the relation R in the set R of real numbers, defined by R = {(a, b) : 1 + ab > 0}, is reflexive, symmetric or transitive.
If Z is the set of all integers and R is the relation on Z defined as R = {(a, b) : a, b ∈ Z and a – b is divisible by 5}. Prove that R is an equivalence relation.
State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} not to be transitive.
Find the particular solution of the differential equation (x – sin y) dy + (tan y) dx = 0, given that y = 0 when x = 0.
Show that the function f:R → R defined by f(x) = is neither one-one nor onto. Also,
if g:R → R is defined as g(x) = 2x – 1, find fog(x).
LetA = {x ∈ Z:0≤ x ≤12}. Show that R={(a,b):a,b ∈ A, |a-b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also write the equivalence class [2].
Find the value of p for which the curves x² = 9p(9 – y) and x² = p(y + 1) cut each other at right angles.
Consider given by f(x) = 5x² + 6x – 9.Prove that f is invertible with f⁻¹(y) = [where, R⁺ is the set of all nonnegative real numbers.]
Solve the differential equation x cos x + sin x, given that y = 1 when
Find the equation of the tangent to the curve which is parallel to the line 4x – 2y + 5 = 0.