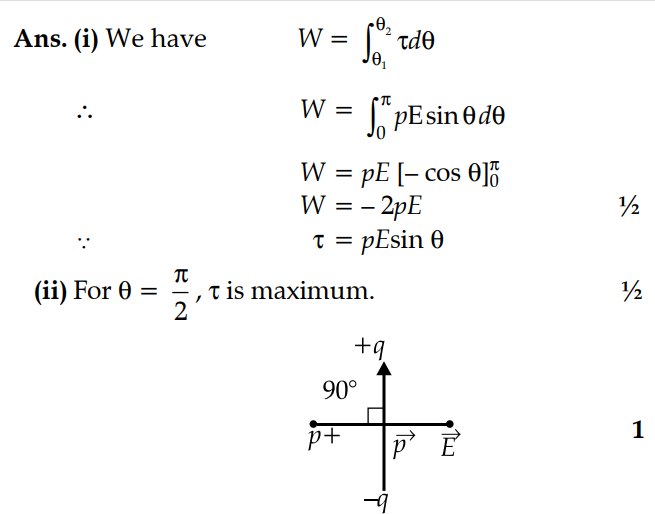
What is the value of the angle between the vectors and for which the potential energy of an electric dipole of dipole moment , kept in an external electric field , has the maximum value.
(i) Obtain the expression for the torque experienced by an electric dipole of dipole moment in a uniform electric field, .
(ii) What will happen if the field were not uniform?
An electric dipole is placed in a uniform electric field.
(i) Show that no translatory force acts on it.
(ii) Derive an expression for the torque acting on it.
(iii) Find work done in rotating the dipole through 180°.
An electric dipole is held in a uniform electric field.
(i) Show that the net force acting on it is zero.
(ii) The dipole is aligned parallel to the field. Find the work done in rotating it through the angle of 180°.
An electric dipole of length 4 cm, when placed with its axis making an angle of 60° with a uniform electric field, experiences a torque of Nm. Calculate the potential energy of the dipole, if it has charge ± 8 nC.
Two dipoles, made from charges ± q and ± Q respectively, have equal dipole moments. Give the
(i) ratio between the ‘separations’ of these two pairs of charges,
(ii) angle between the dipole axes of these two dipoles.
A charge + Q, is uniformly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a distant point r from the centre of the sphere where :
(i) 0 < r < R
(ii) r > R
The figure shows two sinusoidal curves representing oscillating supply voltage and current in an ac circuit.
Find the P.E. associated with a charge q if it were present at the point P with respect to the ‘setup’ of two charged spheres, arranged as shown. Here O is the mid-point of the line O1O2.
Estimate the average drift speed of conduction electrons in a copper wire of cross-sectional area 2.5 × 10⁻⁷ m² carrying a current of 1.8 A. Assume the density of conduction electrons to be 9 × 10²⁸ m⁻³.
The figure shows a plot of terminal voltage ‘V’ versus the current ‘i’ of a given cell. Calculate from the graph
(i) emf of the cell and (ii) internal resistance of the cell.
In a series LCR circuit, obtain the conditions under which
(i) the impedance of the circuit is minimum, and
(ii) wattless current flows in the circuit.
Draw a plot showing the variation of resistivity of a (i) conductor and (ii) semiconductor, with the increase in temperature. How does one explain this behaviour in terms of number density of charge carriers and the relaxation time ?
Using the concept of drift velocity of charge carriers in a conductor, deduce the relationship between current density and resistivity of the conductor.