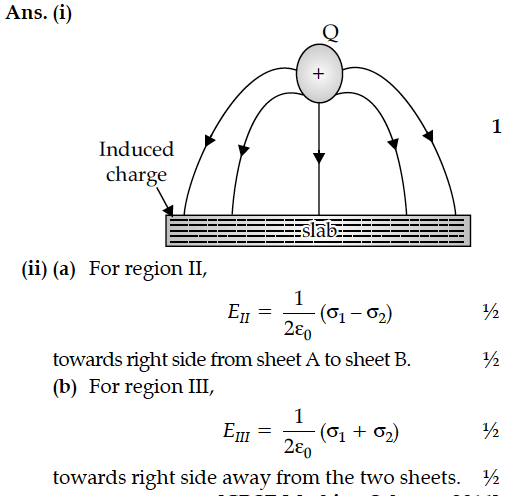
(i) A point charge (+Q) is kept in the vicinity of an uncharged conducting plate. Sketch electric field lines between the charge and the plate.
(ii) Two infinitely large plane thin parallel sheets having surface charge densities σ₁ and σ₂ (σ₁ > σ₂) are shown in the figure. Write the magnitudes and directions of the fields in the regions marked II and III.

(ii) Two infinitely large plane thin parallel sheets having surface charge densities σ₁ and σ₂ (σ₁ > σ₂) are shown in the figure. Write the magnitudes and directions of the fields in the regions marked II and III.

A small metallic sphere carrying charge +Q is located at the centre of a spherical cavity in a large uncharged metallic spherical shell. Write the charges on the inner and outer surfaces of the shell. Write the expression for the electric field at the point P1.
A hollow copper sphere is positively charged. The electric field at its center will be
A. same as that on the surface
B. more than that on the surface
C. less than that on the surface nut not zero
D. zero
A point charge +Q is placed in the vicinity of a conducting surface. Draw the electric field lines between the surface and the charge.
Five charges, q each are placed at the corners of a regular pentagon of side a.
(i) What will be the electric field at O if the charge from one of the corners (say A) is removed ?
(ii) What will be the electric field at O if the charge q at A is replaced by - q ?
A charge + Q, is uniformly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a distant point r from the centre of the sphere where :
(i) 0 < r < R
(ii) r > R
Two point charges ‘q1’ and ‘q2’ are placed at a distance ‘d’ apart as shown in the figure. The electric field intensity is zero at a point ‘P’ on the line joining them as shown. Write two conclusions that you can draw from this.
An electric dipole is held in a uniform electric field.
(i) Show that the net force acting on it is zero.
(ii) The dipole is aligned parallel to the field. Find the work done in rotating it through the angle of 180°.
The potential difference across a resistor ‘r’ carrying current ‘I’ is Ir.
(i) Now if the potential difference across ‘r’ is measured using a voltmeter of resistance ‘’, show that the reading of voltmeter is less than the true value.
(ii) Find the percentage error in measuring the potential difference by a voltmeter.
(iii) At what value of ’, does the voltmeter measures the true potential difference?
A sinusoidal voltage of peak value 10 V is applied to a series LCR circuit in which resistance,capacitance and inductance have values of 10 Ω,1 µF and 1 H respectively. Find
(i) the peak voltage across the inductor at resonance
(ii) quality factor of the circuit.
An electric dipole is placed in a uniform electric field.
(i) Show that no translatory force acts on it.
(ii) Derive an expression for the torque acting on it.
(iii) Find work done in rotating the dipole through 180°.
An inductor of 200 mH, capacitor of 400 µF and a resistor of 10 Ω are connected in series to ac source of 50 V of variable frequency. Calculate the
(a) angular frequency at which maximum power dissipation occurs in the circuit and the corresponding value of the effective current, and
(b) value of Q-factor in the circuit.
Define an equipotential surface. Draw equipotential surfaces :
(i) in the case of a single point charge and
(ii) in a constant electric field in z-direction. Why the equipotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Give reason.
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons ? Use this relation to deduce the expression for the electrical resistivity of the material.
A circuit containing an 80 mH inductor and a 250 µF capacitor in series connected to a 240 V,100 rad/s supply. The resistance of the circuit is negligible.
(i) Obtain rms value of current.
(ii) What is the total average power consumed by the circuit ?
