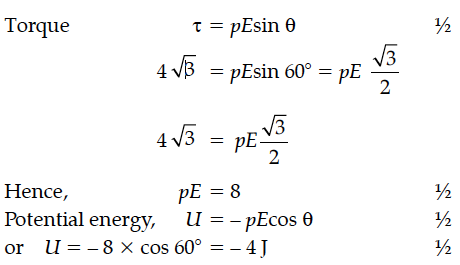
An electric dipole is placed in a uniform electric field.
(i) Show that no translatory force acts on it.
(ii) Derive an expression for the torque acting on it.
(iii) Find work done in rotating the dipole through 180°.
A point charge +Q is placed in the vicinity of a conducting surface. Draw the electric field lines between the surface and the charge.
An electric dipole is held in a uniform electric field.
(i) Show that the net force acting on it is zero.
(ii) The dipole is aligned parallel to the field. Find the work done in rotating it through the angle of 180°.
Derive an expression for electric field of a dipole at a point on the equatorial plane of the dipole. How does the field vary at large distances?
A charge + Q, is uniformly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a distant point r from the centre of the sphere where :
(i) 0 < r < R
(ii) r > R
A charge q is placed at one corner of the cube. The electric flux passing through any one of its face is
Two point charges q1 and q2 are located at points (a, 0, 0) and (0, b, 0) respectively. Find the electric field due to both these charges at the point (0, 0, c).
Calculate the amount of work done to dissociate a system of three charges 1 mC, 1 mC and – 4 mC placed on the vertices of an equilateral triangle of side 10 cm.
Show that the current leads the voltage in phase by in an ac circuit containing an ideal capacitor.
A small metallic sphere carrying charge +Q is located at the centre of a spherical cavity in a large uncharged metallic spherical shell. Write the charges on the inner and outer surfaces of the shell. Write the expression for the electric field at the point P1.
Two point charges q and –2q are kept d distance apart. Find the location of the point relative to charge q at which potential due to this system of charges is zero.
Find the expression for electric field intensity in an axial position due to electric dipole.
The figure shows a series LCR circuit connected to a variable frequency of 200 V source with L = 50 mH, C = 80 µF and R = 40 Ω find.
(i) the source frequency which drives the circuit in resonance;
(ii) the quality factor (Q) of the circuit.
Two cells of E.M.F. 10 V and 2 V and internal resistances 10 Ω and 5 Ω respectively, are connected in parallel as shown. Find the effective voltage across R.