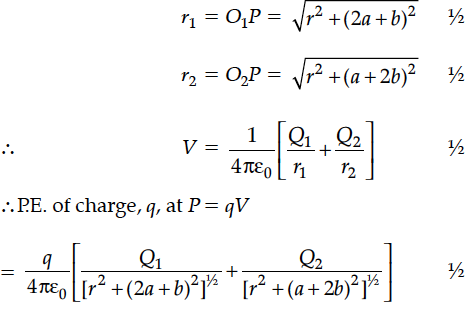
Obtain the expression for the potential due to an electric dipole of dipole moment p at a point ‘d’ on the axial line.
What is the amount of work done in moving a point charge around a circular arc of radius r at the center where another point charge is located ?
Why must electrostatic field at the surface of a charged conductor be normal to the surface at every point ? Give reason.
Draw a plot showing the variation of (i) electric field (E) and (ii) electric potential (V) with distance r due to a point charge Q.
A point charge +Q is placed at point O as shown in the figure. Is the potential difference – positive, negative or zero ?
Figure shows the field lines due to a positive charge. Is the work done by the field in moving a small positive charge from Q to P, positive or negative? Give reason.
An electron is accelerated through a potential difference V. Write the expression for its final speed, if it was initially at rest.
A network of resistors is connected to a 16 V battery with internal resistance of 1 Ω, as shown in the following figure. Compute the equivalent resistance of the network.
Two metallic wires P₁ and P₂ of the same material and same length but different cross-sectional areas A₁ and A₂ are joined together and then connected to a source of emf. Find the ratio of the drift velocities of free electrons in the wires P₁ and P₂ if the wires are connected
(i) in series, and (ii) in parallel.
A lamp is connected in series with a capacitor. Predict your observation for dc and ac connections. What happens in each if the capacitance of the capacitor is reduced ?
Two closely spaced equipotential surfaces A and B with potentials V and V + , (where is the change in V), are kept distance apart as shown in the figure. Deduce the relation between the electric field and the potential gradient between them. Write the two important conclusions concerning the relation between the electric field and electric potentials.
In the circuit shown in the figure, find the current through each resistor.
Three concentric metallic shells A, B and C of radii a, b and c (a < b < c) have surface charge densities +σ, –σ and +σ respectively as shown in the figure.
Two point charges q and –2q are kept d distance apart. Find the location of the point relative to charge q at which potential due to this system of charges is zero.