An ac voltage V = V₀ sin ωt is applied to a pure inductor L. Obtain an expression for the current in the circuit. Prove that the average power supplied to an inductor over one complete cycle is zero.
(i) If an alternating voltage V = V₀ sin ωt is applied across pure inductor of inductance L, then the magnitude of induced emf will be equal to applied voltage,
E = L (dI/dt)
For the circuit, magnitude of induced emf = applied voltage
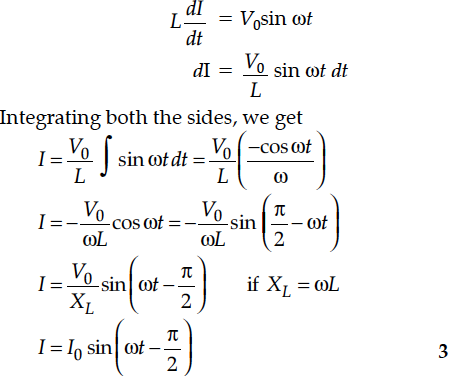

E = L (dI/dt)
For the circuit, magnitude of induced emf = applied voltage
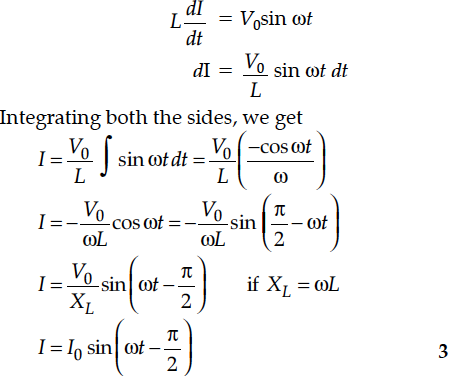

A source of ac voltage V = V₀ sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time.
A 40 mF capacitor is connected to a 200 V, 50 Hz ac supply. The r.m.s value of the current in the circuit is, nearly
(a) 1.7 A
(b) 2.05 A
(c) 2.5 A
(d) 25.1 A
State which of the two a capacitor or an inductor, tends to become SHORT when the frequency of the applied alternating voltage has a high value.
In a series LCR circuit, obtain the conditions under which
(i) the impedance of the circuit is minimum, and
(ii) wattless current flows in the circuit.
A lamp is connected in series with a capacitor. Predict your observation for dc and ac connections. What happens in each if the capacitance of the capacitor is reduced ?
Obtain the expression for the energy density of magnitude field B produced in the inductor.
(i) Two isolated metal spheres A and B have radii R and 2R respectively, and same charge q. Find which of the two spheres have greater :
(a) capacitance and
(b) energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the regions of weak field. Draw equipotential surfaces for an electric dipole.
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.
In the following circuit, calculate (i) the capacitance of the capacitor, if the power factor of the circuit is unity, (ii) the Q-factor of this circuit. What is the significance of the Q-factor in ac circuit ? Given the angular frequency of the ac source to be 100rad/s. Calculate the average power dissipated in the circuit.
A device X is connected across an ac source of voltage V = V₀ sin ωt. The current through X is given as I = I₀sin(ωt +π/2).
(a) Identify the device X and write the expression for its reactance.
(b) Draw graphs showing variation of voltage and current with time over one cycle of ac, for X.
(c) How does the reactance of the device X vary with frequency of the ac ? Show this variation graphically.
(d) Draw the phasor diagram for the device X.
(i) Obtain the expression for the potential to show due to a point charge.
(ii) Potential, due to an electric dipole (length 2a) varies as the ‘inverse square’ of the distance of the ‘field point’ from the centre of the dipole for r > a.
An ac voltage V = V₀ sin ωt is applied to a pure inductor L. Obtain an expression for the current in the circuit. Prove that the average power supplied to an inductor over one complete cycle is zero.
(i) An ac source generating a voltage V = V₀ sin ωt is connected to a capacitor of capacitance C. Find the expression of the current I flowing through it.Plot a graph of V and I versus ωt to show that the current is π/2
ahead of the voltage.
(ii) A resistor of 200Ω and a capacitor of 15 µF are connected in series to a 220 V, 50 Hz ac source.Calculate the current in the circuit and the rms
voltage across the resistor and the capacitor. Why the algebraic sum of these voltages is more than the source voltage ?
Derive an expression for potential due to a dipole for distances large compared to the size of the dipole. How is the potential due to dipole different from that due to single charge ?
