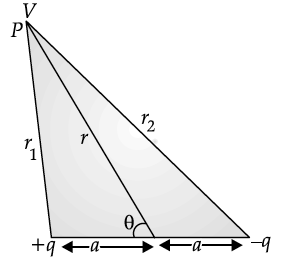
Obtain the expression for the potential due to an electric dipole of dipole moment p at a point ‘d’ on the axial line.
(i) Derive the expression for the electric potential due to an electric dipole at a point on its axial line.
(ii) Depict the equipotential surface due to electric dipole.
Draw a plot showing the variation of (i) electric field (E) and (ii) electric potential (V) with distance r due to a point charge Q.
Electric potential at a distance r from the point charge is proportional to
1. \(r^2\)
2. r-1
3. r0
4. r+1
Two point charges q and –2q are kept d distance apart. Find the location of the point relative to charge q at which potential due to this system of charges is zero.
A charge ‘q’ is moved from a point A above a dipole of dipole moment ‘p’ to a point B below the dipole in equatorial plane without acceleration. Find the work done in the process.
An electron is accelerated through a potential difference V. Write the expression for its final speed, if it was initially at rest.
A device ‘X’ is connected to an ac source V = The variation of voltage, current and power in one cycle is shown in the following graph :
(i) An ac source generating a voltage V = V₀ sin ωt is connected to a capacitor of capacitance C. Find the expression of the current I flowing through it.Plot a graph of V and I versus ωt to show that the current is π/2 ahead of the voltage.
(ii) A resistor of 200Ω and a capacitor of 15 µF are connected in series to a 220 V, 50 Hz ac source.Calculate the current in the circuit and the rms
voltage across the resistor and the capacitor. Why the algebraic sum of these voltages is more than the source voltage ?
A device X is connected across an ac source of voltage V = V₀ sin ωt. The current through X is given as I = I₀sin(ωt +π/2).
(a) Identify the device X and write the expression for its reactance.
(b) Draw graphs showing variation of voltage and current with time over one cycle of ac, for X.
(c) How does the reactance of the device X vary with frequency of the ac ? Show this variation graphically.
(d) Draw the phasor diagram for the device X.
Derive an expression for potential due to a dipole for distances large compared to the size of the dipole. How is the potential due to dipole different from that due to single charge ?
(i) Two isolated metal spheres A and B have radii R and 2R respectively, and same charge q. Find which of the two spheres have greater :
(a) capacitance and
(b) energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the regions of weak field. Draw equipotential surfaces for an electric dipole.
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.
(i) Obtain the expression for the potential to show due to a point charge.
(ii) Potential, due to an electric dipole (length 2a) varies as the ‘inverse square’ of the distance of the ‘field point’ from the centre of the dipole for r > a.
Two point charges q and –q are located at points (0, 0, – a) and (0, 0, a) respectively.
(i) Find the electrostatic potential at (0, 0, z) and (x, y, 0).
(ii) How much work is done in moving a small test charge from the point (5,0,0) to (– 7, 0, 0) along the x-axis ?
(iii) How would your answer change if the path of the test charge between the same points is not along the x-axis but along any other random path ?
(iv) If the above point charges are now placed in the same positions in the uniform external electric field what would be the potential energy of the charge system in its orientation of unstable equilibrium ?
Justify your answer in each case.