(i) An ac source generating a voltage V = V₀ sin ωt is connected to a capacitor of capacitance C. Find the expression of the current I flowing through it.Plot a graph of V and I versus ωt to show that the current is π/2
ahead of the voltage.
(ii) A resistor of 200Ω and a capacitor of 15 µF are connected in series to a 220 V, 50 Hz ac source.Calculate the current in the circuit and the rms
voltage across the resistor and the capacitor. Why the algebraic sum of these voltages is more than the source voltage ?
(ii) A resistor of 200Ω and a capacitor of 15 µF are connected in series to a 220 V, 50 Hz ac source.Calculate the current in the circuit and the rms
voltage across the resistor and the capacitor. Why the algebraic sum of these voltages is more than the source voltage ?
An alternating voltage E = E₀ sin ωt is applied to the circuit containing a resistor R connected in series with a black box. The current in the circuit is found to be I=I₀ (sin ωt+π/4)
(i) When an ac source is connected to an ideal capacitor show that the average power supplied by the source over a complete cycle is zero.
(ii) A lamp is connected in series with a capacitor.Predict your observation when the system is connected first across a dc and then an ac source.What happens in each case if the capacitance of the capacitor is reduced ?
(i) When an ac source is connected to an ideal inductor shows that the average power supplied by the source over a complete cycle is zero.
(ii) A lamp is connected in series with an inductor and an ac source. What happens to the brightness of the lamp when the key is plugged in and an iron rod is inserted inside the inductor ? Explain.
(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?
(ii) Without making any other change, find the value of the additional capacitor C₁, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
A source of ac voltage V = V₀ sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
A voltage V = V₀ sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipate over a cycle.Under what conditions is
(i) no power dissipated even though the current flows through the circuit,
(ii)maximum power dissipated in the circuit ?
A small signal voltage V(t) = V₀ sin(ωt) is applied across an ideal capacitor C
(a) Current I(t) is in phase with voltage V(t).
(b) Current I(t) leads voltage V(t) by 180°.
(c) Current I(t), lags voltage V(t) by 90°.
(d) Over a full cycle the capacitor C does not consume any energy from the voltage source
(i) Two isolated metal spheres A and B have radii R and 2R respectively, and same charge q. Find which of the two spheres have greater :
(a) capacitance and
(b) energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the regions of weak field. Draw equipotential surfaces for an electric dipole.
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.
A device ‘X’ is connected to an ac source V = The variation of voltage, current and power in one cycle is shown in the following graph :
Derive an expression for potential due to a dipole for distances large compared to the size of the dipole. How is the potential due to dipole different from that due to single charge ?
(a) Draw graphs showing the variations of inductive reactance and capacitive reactance with frequency of the applied ac source.
(b) Draw the phasor diagram for a series RC circuit connected to an ac source.
(c) An alternating voltage of 220 V is applied across a device X, a current of 0.25 A flows, which lag behind the applied voltage in phase by π/2
radian.If the same voltage is applied across another device Y, the same current flows but now it is in phase with the applied voltage.
(i) Name the devices X and Y.
(ii) Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
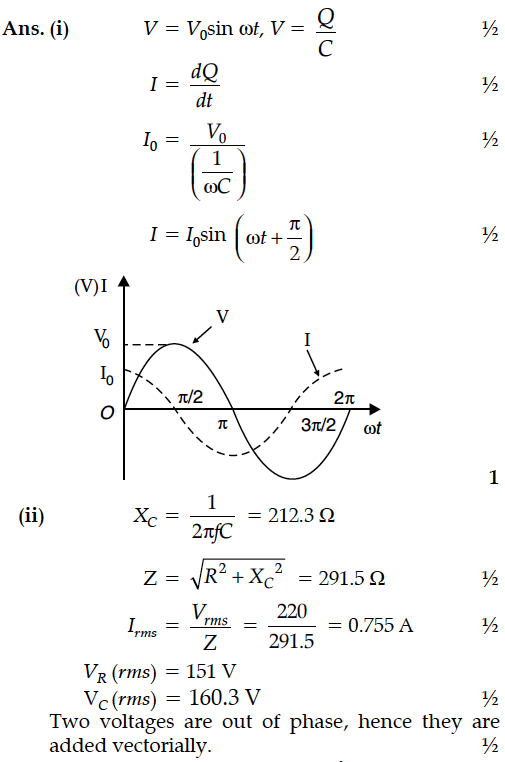
(i) An ac source generating a voltage V = V₀ sin ωt is connected to a capacitor of capacitance C. Find the expression of the current I flowing through it.Plot a graph of V and I versus ωt to show that the current is π/2
ahead of the voltage.
(ii) A resistor of 200Ω and a capacitor of 15 µF are connected in series to a 220 V, 50 Hz ac source.Calculate the current in the circuit and the rms
voltage across the resistor and the capacitor. Why the algebraic sum of these voltages is more than the source voltage ?
(i) Why do the 'free electrons', in a metal wire, 'flowing by themselves', not cause any current flow in the wire ?
Define 'drift velocity' and obtain an expression for the current flowing in a wire, in terms of the 'drift velocity' of the free electrons.
(ii) Use the above expression to show that the 'resistivity', of the material of a wire, is inversely proportional to the 'relaxation time' for the 'free electrons' in the metal.
An ac voltage V = V₀ sin ωt is applied to a pure inductor L. Obtain an expression for the current in the circuit. Prove that the average power supplied to an inductor over one complete cycle is zero.
