(i) Two isolated metal spheres A and B have radii R and 2R respectively, and same charge q. Find which of the two spheres have greater :
(a) capacitance and
(b) energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the regions of weak field. Draw equipotential surfaces for an electric dipole.
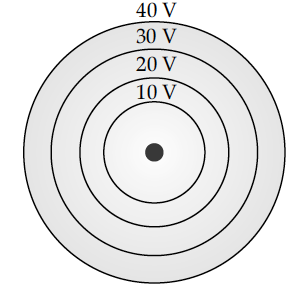
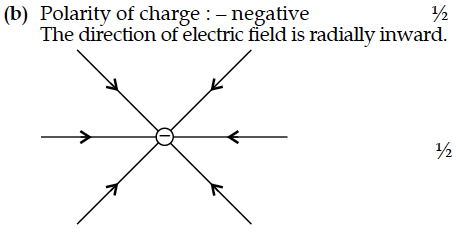
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.
(a) capacitance and
(b) energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the regions of weak field. Draw equipotential surfaces for an electric dipole.
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.


(i) Three point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side ‘l’ as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
Two closely spaced equipotential surfaces A and B with potentials V and V + , (where is the change in V), are kept distance apart as shown in the figure. Deduce the relation between the electric field and the potential gradient between them. Write the two important conclusions concerning the relation between the electric field and electric potentials.
A Solid conducting sphere having a charge Q is surrounded by an uncharged concentric conducting spherical shell. Let the potential difference between the surface of the solid sphere and the outer of the shell be V. If the shell is given a charge -3Q the new potential difference between the same two surfaces is
1. 2V
2. V/2
3. V
4. -2V
Define an equipotential surface. Draw equipotential surfaces :
(i) in the case of a single point charge and
(ii) in a constant electric field in z-direction. Why the equipotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Give reason.
Write two properties of equipotential surfaces. Depict equipotential surfaces due to an isolated point charge. Why do the equipotential surfaces get closer as the distance between the equipotential surfaces and the source charge decreases ?
(i) Write two properties by which electric potential is related to the electric field.
(ii) Two point charges q₁ and q₂ separated by a distance of r₁₂ are kept in an external electric field. Derive an expression for the potential energy of the system of two charges in the field.
A particle, having a charge +5 µC, is initially at rest at the point x = 30 cm on the x-axis. The particle begins to move due to the presence of a charge Q that is kept fixed at the origin. Find the kinetic energy of the particle at the instant it has moved 15 cm from its initial position if
(a) Q = +15 µC and
(b) Q = – 15 µC
Two point charges q and –q are located at points (0, 0, – a) and (0, 0, a) respectively.
(i) Find the electrostatic potential at (0, 0, z) and (x, y, 0).
(ii) How much work is done in moving a small test charge from the point (5,0,0) to (– 7, 0, 0) along the x-axis ?
(iii) How would your answer change if the path of the test charge between the same points is not along the x-axis but along any other random path ?
(iv) If the above point charges are now placed in the same positions in the uniform external electric field what would be the potential energy of the charge system in its orientation of unstable equilibrium ?
Justify your answer in each case.
(i) An ac source generating a voltage V = V₀ sin ωt is connected to a capacitor of capacitance C. Find the expression of the current I flowing through it.Plot a graph of V and I versus ωt to show that the current is π/2
ahead of the voltage.
(ii) A resistor of 200Ω and a capacitor of 15 µF are connected in series to a 220 V, 50 Hz ac source.Calculate the current in the circuit and the rms
voltage across the resistor and the capacitor. Why the algebraic sum of these voltages is more than the source voltage ?
Derive an expression for potential due to a dipole for distances large compared to the size of the dipole. How is the potential due to dipole different from that due to single charge ?
(i) Prove that current flowing through an ideal inductor connected across ac source, lags the voltage in phase by .
(ii) An inductor of self inductance 100 mH, and a bulb are connected in series with ac source of rms voltage 10V, 50 Hz. It is found that effective voltage of the circuit leads the current in phase by .Calculate the inductance of the inductor used and average power dissipated in the circuit, if a current of 1 A flows in the circuit.
(i) Why do the 'free electrons', in a metal wire, 'flowing by themselves', not cause any current flow in the wire ?
Define 'drift velocity' and obtain an expression for the current flowing in a wire, in terms of the 'drift velocity' of the free electrons.
(ii) Use the above expression to show that the 'resistivity', of the material of a wire, is inversely proportional to the 'relaxation time' for the 'free electrons' in the metal.
(i) Two isolated metal spheres A and B have radii R and 2R respectively, and same charge q. Find which of the two spheres have greater :
(a) capacitance and
(b) energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the regions of weak field. Draw equipotential surfaces for an electric dipole.
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.
In the following circuit, calculate (i) the capacitance of the capacitor, if the power factor of the circuit is unity, (ii) the Q-factor of this circuit. What is the significance of the Q-factor in ac circuit ? Given the angular frequency of the ac source to be 100rad/s. Calculate the average power dissipated in the circuit.
