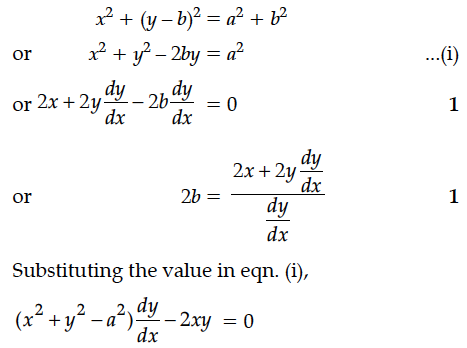
Form the differential equation of all circles which is tough the x-axis at the origin.
Form the differential equation of the family of circles in the second quadrant and touching the co-ordinate axes.
From the differential equation of equation y = a cos 2x + b sin 2x, where a and b are constant.
Form the differential equation representing family of ellipses having foci on X-axis and centre at the origin.
If P(F) = 0·35 and P(E U F) = 0·85 and E and F are independent events. Find P(E).
If x changes from 4 to 4·01, then find the approximate change in log x.
From the differential equation of equation y = a cos 2x + b sin 2x, where a and b are constant.
