Form the differential equation representing family of ellipses having foci on X-axis and centre at the origin.
We know that, the equation of family of ellipse having foci on X-axis and centre at origin is given by 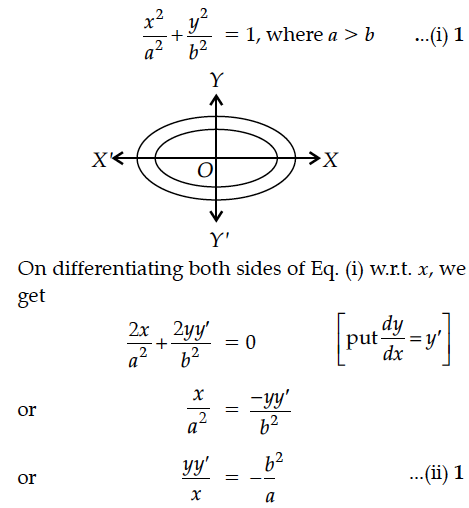



Form the differential equation of all circles which is tough the x-axis at the origin.
Form the differential equation representing family of curves given by (x – a)² + 2y²= a², where a is an arbitrary constant.
Form the differential equation of the family of circles in the second quadrant and touching the co-ordinate axes.
Find the differential equation representing the family of curves where A and B are arbitrary constants.
From the differential equation of equation y = a cos 2x + b sin 2x, where a and b are constant.
Obtain the differential equation of the family of circles passing through the points (a, 0) and (– a, 0).
Prove that the function f : [0, ∞) → R given by f(x) = 9x² + 6x – 5 is not invertible. Modify the Codomain of the function f to make it invertible, and hence find f⁻¹.
A speaks truth in 60% of the cases, while B in 90% of cases. In what percent of cases are they likely to contradict each other in stating the same fact ? In the cases of contradiction do you think, the statement of B will carry more weight as he speaks truth in more number of cases than A ?
The total cost associated with provision of free mid-day meals to x students of a school in primary classes is given by C(x) = 0·005x³ – 0·02x² + 30x + 50. If the marginal cost is given by rate of change of total cost, write the marginal cost of food for 300 students.
Let R be a relation defined on the set of natural numbers N as follow :
R = {(x, y) : and 2x + y = 24}
Find the domain and range of the relation R. Also,find if R is an equivalence relation or not.
