If P(E) = 1/2, and P(F) = 1/5 find P(E U F)' if E and F are independent events.
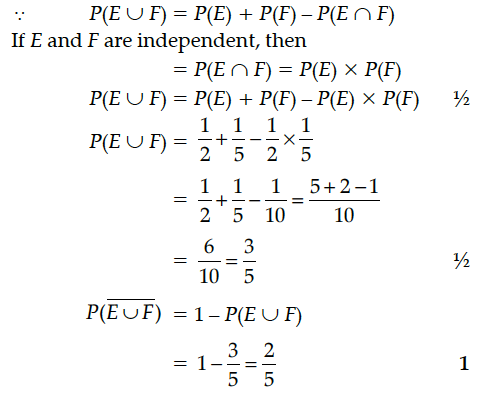
If E and F be two events such that P(E) = 1/3, P(F) = 1/4, find P(E U F) if E and F are independent events.
Show that the function f given by f(x) = tan⁻¹ (sin x+ cos x) is decreasing for all
If P(E) = 6/11, P(F) = 5/11 and P(E ∪ F) = 7/11 then find
(i) P(E/F)
(ii) P(F/E)
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy
(ii) the older child is a boy.
If E and F be two events such that P(E) = 1/3, P(F) = 1/4, find P(E U F) if E and F are independent events.
The radius r of a right circular cylinder is increasing uniformly at the rate of 0.3 cm/s and its height h is decreasing at the rate of 0.4 cm/s. When r = 3.5 cm and h = 7 cm, find the rate of change of the curved surface area of the cylinder.
