If P(F) = 0·35 and P(E U F) = 0·85 and E and F are independent events. Find P(E).
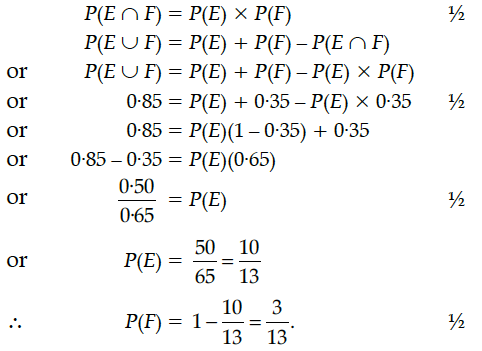
If P(A) = 0.4, P(B) = p, P(A U B) = 0.6 and A and B are given to the independent events, find the value of ‘p’.
Find the inverse of the matrix Hence, find the matrix P satisfying the matrix equation P = .
Show that the function f(x) = x³ – 3x² + 6x – 100 is increasing on R.
If P(A) = 0.4, P(B) = p, P(A U B) = 0.6 and A and B are given to the independent events, find the value of ‘p’.
A die is rolled. If E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}, find
(a) P(E U F)/G]
(b)P [(E ∩ F)/G].
