Find the differential equation of the family of lines passing through the origin.
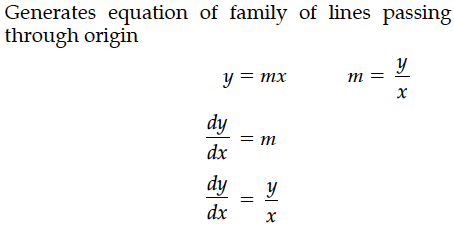
Obtain the differential equation of the family of circles passing through the points (a, 0) and (– a, 0).
Form the differential equation of all circles which is tough the x-axis at the origin.
From the differential equation of equation y = a cos 2x + b sin 2x, where a and b are constant.
Form the differential equation of the family of circles in the second quadrant and touching the co-ordinate axes.
Form the differential equation representing family of ellipses having foci on X-axis and centre at the origin.
State the reason why the Relation R = {(a, b) : a ≤ b²} on the set R of real numbers is not reflexive.
If A = is is a matrix of order 2 × 2, such that |A| = –15, and represents the cofactor of , then find
If A = {1, 2, 3}, B = {4, 5, 6, 7} and f = {(1, 4), (2, 5),(3, 6)} is a function from A to B. State whether f is one-one or not.
Find the scalar components of the vector with initial point A(2,1) and terminal point B (– 5, 7).
