From the differential equation of equation y = a cos 2x + b sin 2x, where a and b are constant.
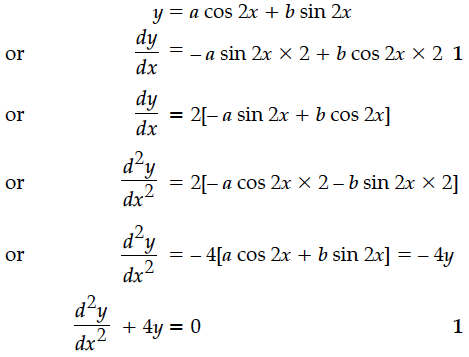
Write the differential equation formed from the equation y = mx + c, where m and c are arbitrary constants.
Form the differential equation of all circles which is tough the x-axis at the origin.
Form the differential equation of the family of circles in the second quadrant and touching the co-ordinate axes.
Show that the function f(x) = x³ – 3x² + 6x – 100 is increasing on R.
The radius r of the base of a right circular cone is decreasing at the rate of 2 cm/min. and height h is increasing at the rate of 3 cm/min. When r = 3.5 cm and h = 6 cm, find the rate of change of the volume of the cone.
Find the sum of the order and the degree of the following differential equations :
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy
(ii) the older child is a boy.
Three cards are drawn without replacement from a pack of 52 cards. Find the probability that
(i) the cards drawn are king, queen and jack respectively.
(ii) the cards drawn are king, queen and jack.
