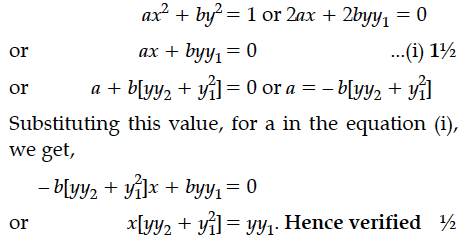Question

A balloon, which always remains spherical, has a variable diameter ${\frac{2}{3}}(3x+1)$ . Find the rate of change of its volume with respect to x.

Form the differential equation of all circles which is tough the x-axis at the origin.

Verify that ax² + by² = 1 is a solution of differential equation $x(y y_{2}+y_{1}^{2})=y y_{1}.$

Find : $\textstyle\int$$\sqrt{2x-x^{2}\ d x}$

Show that the function f(x) = x³ – 3x² + 6x – 100 is increasing on R.

Find the sum of the order and the degree of the following differential equations : ${\frac{d^{2}y}{d x^{2}}}+{3{\sqrt\frac{{d y}}{d x}}}+(1+x)=0$

If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’)