Show that the function f(x) = x³ – 3x² + 6x – 100 is increasing on R.
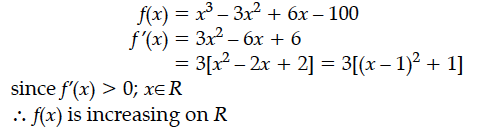
Show that the equation of tangent to the parabola y² = 4ax at (x₁, y₁) is yy₁ = 2a(x + x₁).
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
A die is rolled. If E = {1, 3, 5}, F = {2, 3} and G = {2, 3, 4, 5}, find
(a) P(E U F)/G]
(b)P [(E ∩ F)/G].
A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green, is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events.
The length x, of a rectangle is decreasing at the rate of 5 cm/minute and the width y, is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rate of change of the area of the rectangle.
The radius r of the base of a right circular cone is decreasing at the rate of 2 cm/min. and height h is increasing at the rate of 3 cm/min. When r = 3.5 cm and h = 6 cm, find the rate of change of the volume of the cone.
If E and F are two events such that P(E) = 1/4, P(F) = 1/2 and P(E ∩ F) = 1/8, find
(i) P(E or F)
(ii) P(not E and not F).
