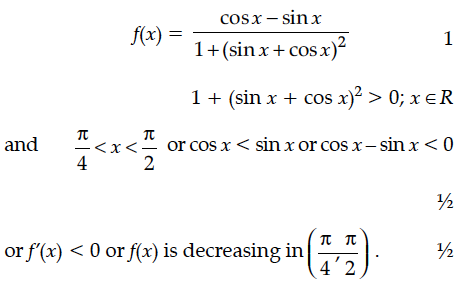
Find the equations of tangents to the curve 3x² – y² = 8, which passes through the point
Find the equation of tangent and normal to the curve x = 1 – cos θ, y = θ – sin θ at θ =
Find the equations of the tangent and normal to the curve x = a sin³θ, y = b cos³θ at
Show that the equation of tangent to the parabola y² = 4ax at (x₁, y₁) is yy₁ = 2a(x + x₁).
If P(E) = 6/11, P(F) = 5/11 and P(E ∪ F) = 7/11 then find
(i) P(E/F)
(ii) P(F/E)
If E and F are two events such that P(E) = 1/4, P(F) = 1/2 and P(E ∩ F) = 1/8, find
(i) P(E or F)
(ii) P(not E and not F).
Find the differential equation of the family of curves y²= 4ax.
If E and F are independent events, then show that
(i) E and F' are independent events.
(ii) E' and F are also independent events.