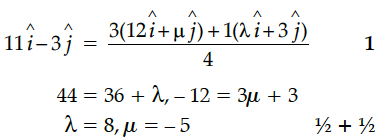
The two vectors and represent the two sides AB and AC, respectively of Find the length of the median through A.
Find the particular solution of the differential equation given that y(0) =
Obtain the differential equation of the family of circles passing through the points (a, 0) and (– a, 0).
If P(E) = 6/11, P(F) = 5/11 and P(E ∪ F) = 7/11 then find
(i) P(E/F)
(ii) P(F/E)
The radius r of a right circular cylinder is decreasing at the rate of 3 cm/min. and its height h is increasing at the rate of 2 cm/min. When r =7 cm and h = 2 cm, find the rate of change of the volume of cylinder.
If A and B are two independent events, prove that A’ and B are also independent.