Define an equipotential surface. Draw equipotential surfaces :
(i) in the case of a single point charge and
(ii) in a constant electric field in z-direction. Why the equipotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Give reason.
(i) in the case of a single point charge and
(ii) in a constant electric field in z-direction. Why the equipotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Give reason.
Equipotential surface is a surface which has equal potential at every point on it.
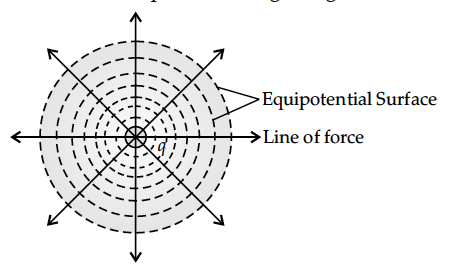
(i) Equipotential surfaces due to single point charge are concentric spheres having charge at the centre.
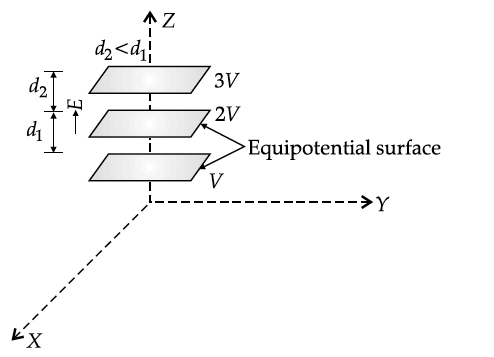
(ii) In constant electric field along z-direction, the perpendicular distance between equipotential surfaces remains same.
For single charge, equipotential surface will be series of concentric spherical shells with charge at centre,
the separation dr between equipotential surfaces will go on increasing with decrease in electric field.
(iii) No, because if the surface is not equipotential then it would mean that there is tangential component of electric field along surface. This component will result in motion of electrons, but since we have static fields, this is not possible.
(i) Equipotential surfaces due to single point charge are concentric spheres having charge at the centre.

(ii) In constant electric field along z-direction, the perpendicular distance between equipotential surfaces remains same.

For single charge, equipotential surface will be series of concentric spherical shells with charge at centre,
the separation dr between equipotential surfaces will go on increasing with decrease in electric field.
(iii) No, because if the surface is not equipotential then it would mean that there is tangential component of electric field along surface. This component will result in motion of electrons, but since we have static fields, this is not possible.
Write two properties of equipotential surfaces. Depict equipotential surfaces due to an isolated point charge. Why do the equipotential surfaces get closer as the distance between the equipotential surfaces and the source charge decreases ?
In a region of constant potential,
(a) the electric field is uniform
(b) the electric field is zero
(c) there can be no charge inside the region
(d) the electric field shall necessarily change, if a charge is placed outside the region
For any charge configuration equipotential surface through a point is normal to the electric field.
1. Since W=Fscosθ is zero so field is normal to the surface
2. As W≠0
3. Work done can be Zero if Field is parallel to the field
4. None of these
(i) Obtain the expression for the potential to show due to a point charge.
(ii) Potential, due to an electric dipole (length 2a) varies as the ‘inverse square’ of the distance of the ‘field point’ from the centre of the dipole for r > a.
Derive an expression for potential due to a dipole for distances large compared to the size of the dipole. How is the potential due to dipole different from that due to single charge ?
(i) Derive the expression for the electric potential due to an electric dipole at a point on its axial line.
(ii) Depict the equipotential surface due to electric dipole.
Equipotential surfaces at a great distance from a collection of charges whose total sum is not zero are approximately
(a) spheres
(b) planes
(c) paraboloids
(d) ellipsoids
A circuit containing an 80 mH inductor and a 250 µF capacitor in series connected to a 240 V,100 rad/s supply. The resistance of the circuit is negligible.
(i) Obtain rms value of current.
(ii) What is the total average power consumed by the circuit ?
(i) Derive an expression for drift velocity of electrons in a conductor. Hence deduce Ohm’s law.
(ii) A wire whose cross-sectional area is increasing linearly from its one end to the other, is connected across a battery of V volts. Which of the following quantities remain constant in the wire ?
(a) drift speed
(b) current density
(c) electric current
(d) electric field
Justify your answer.
(i) The potential difference applied across a given resistor is altered so that the heat produced per second increases by a factor of 9. By what factor does the applied potential difference change ?
(ii) In the figure shown, an ammeter A and a resistor of 4 W are connected to the terminals of the source. The emf of the source is 12 V having an internal resistance of 2 W. Calculate the voltmeter and ammeter readings.
(i) Derive the expression for electric field at a point on the equatorial line of an electric dipole.
(ii) Depict the orientation of the dipole in (i) stable, (ii) unstable equilibrium in a uniform electric field.
Define relaxation time of the free electrons drifting in a conductor. How is it related to the drift velocity of free electrons ? Use this relation to deduce the expression for the electrical resistivity of the material.
A source of ac voltage V = V₀ sin ωt is connected to a series combination of a resistor ‘R’ and a capacitor ‘C’. Draw the phasor diagram and use it to obtain the expression for
(i) impedance of the circuit and
(ii) phase angle.
(i) Three point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side ‘l’ as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
