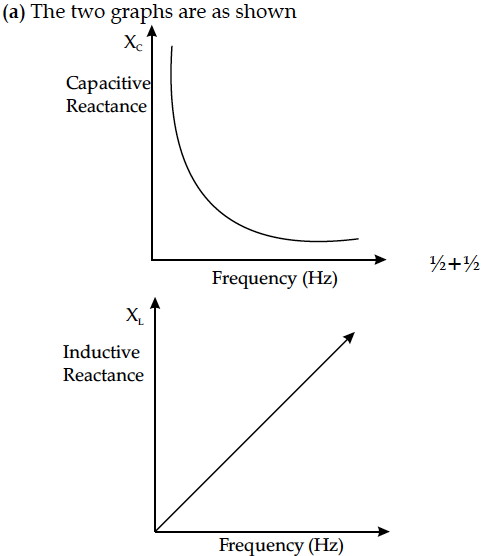
(a) Draw graphs showing the variations of inductive reactance and capacitive reactance with frequency of the applied ac source.
(b) Draw the phasor diagram for a series RC circuit connected to an ac source.
(c) An alternating voltage of 220 V is applied across a device X, a current of 0.25 A flows, which lag behind the applied voltage in phase by π/2 radian.If the same voltage is applied across another device Y, the same current flows but now it is in phase with the applied voltage.
(i) Name the devices X and Y.
(ii) Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
(b) Draw the phasor diagram for a series RC circuit connected to an ac source.
(c) An alternating voltage of 220 V is applied across a device X, a current of 0.25 A flows, which lag behind the applied voltage in phase by π/2 radian.If the same voltage is applied across another device Y, the same current flows but now it is in phase with the applied voltage.
(i) Name the devices X and Y.
(ii) Calculate the current flowing in the circuit when the same voltage is applied across the series combination of X and Y.
(a) Drawing the two graphs ½+½
(b) Drawing the phaser diagram 1
(c) (i) Naming the devices ½+½
(ii) Calculating the current flowing 2
(b) Drawing the phaser diagram 1
(c) (i) Naming the devices ½+½
(ii) Calculating the current flowing 2

(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?
(ii) Without making any other change, find the value of the additional capacitor C₁, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
The current, in the LCR circuit shown in the figure is observed to lead the voltage in phase. Without making any other change in the circuit, a capacitor,of capacitance C₀, is (appropriately) joined to the capacitor C. This results in making the current,in the ‘modified’ circuit, flow in phase with theapplied voltage.
Draw a diagram of the ‘modified’ circuit and obtain an expression for C₀ in terms of ω, L and C.
(i) An ac source generating a voltage V = V₀ sin ωt is connected to a capacitor of capacitance C. Find the expression of the current I flowing through it.Plot a graph of V and I versus ωt to show that the current is π/2
ahead of the voltage.
(ii) A resistor of 200Ω and a capacitor of 15 µF are connected in series to a 220 V, 50 Hz ac source.Calculate the current in the circuit and the rms
voltage across the resistor and the capacitor. Why the algebraic sum of these voltages is more than the source voltage ?
(i) Prove that current flowing through an ideal inductor connected across ac source, lags the voltage in phase by .
(ii) An inductor of self inductance 100 mH, and a bulb are connected in series with ac source of rms voltage 10V, 50 Hz. It is found that effective voltage of the circuit leads the current in phase by .Calculate the inductance of the inductor used and average power dissipated in the circuit, if a current of 1 A flows in the circuit.
In the following circuit, calculate (i) the capacitance of the capacitor, if the power factor of the circuit is unity, (ii) the Q-factor of this circuit. What is the significance of the Q-factor in ac circuit ? Given the angular frequency of the ac source to be 100rad/s. Calculate the average power dissipated in the circuit.
A device X is connected across an ac source of voltage V = V₀ sin ωt. The current through X is given as I = I₀sin(ωt +π/2).
(a) Identify the device X and write the expression for its reactance.
(b) Draw graphs showing variation of voltage and current with time over one cycle of ac, for X.
(c) How does the reactance of the device X vary with frequency of the ac ? Show this variation graphically.
(d) Draw the phasor diagram for the device X.
(i) When an ac source is connected to an ideal inductor shows that the average power supplied by the source over a complete cycle is zero.
(ii) A lamp is connected in series with an inductor and an ac source. What happens to the brightness of the lamp when the key is plugged in and an iron rod is inserted inside the inductor ? Explain.
(i) An ac source generating a voltage V = V₀ sin ωt is connected to a capacitor of capacitance C. Find the expression of the current I flowing through it.Plot a graph of V and I versus ωt to show that the current is π/2
ahead of the voltage.
(ii) A resistor of 200Ω and a capacitor of 15 µF are connected in series to a 220 V, 50 Hz ac source.Calculate the current in the circuit and the rms
voltage across the resistor and the capacitor. Why the algebraic sum of these voltages is more than the source voltage ?
Derive an expression for potential due to a dipole for distances large compared to the size of the dipole. How is the potential due to dipole different from that due to single charge ?
An ac voltage V = V₀ sin ωt is applied to a pure inductor L. Obtain an expression for the current in the circuit. Prove that the average power supplied to an inductor over one complete cycle is zero.
(i) Obtain the expression for the potential to show due to a point charge.
(ii) Potential, due to an electric dipole (length 2a) varies as the ‘inverse square’ of the distance of the ‘field point’ from the centre of the dipole for r > a.
(i) Prove that current flowing through an ideal inductor connected across ac source, lags the voltage in phase by .
(ii) An inductor of self inductance 100 mH, and a bulb are connected in series with ac source of rms voltage 10V, 50 Hz. It is found that effective voltage of the circuit leads the current in phase by .Calculate the inductance of the inductor used and average power dissipated in the circuit, if a current of 1 A flows in the circuit.
A device ‘X’ is connected to an ac source V = The variation of voltage, current and power in one cycle is shown in the following graph :
Two point charges q and –q are located at points (0, 0, – a) and (0, 0, a) respectively.
(i) Find the electrostatic potential at (0, 0, z) and (x, y, 0).
(ii) How much work is done in moving a small test charge from the point (5,0,0) to (– 7, 0, 0) along the x-axis ?
(iii) How would your answer change if the path of the test charge between the same points is not along the x-axis but along any other random path ?
(iv) If the above point charges are now placed in the same positions in the uniform external electric field what would be the potential energy of the charge system in its orientation of unstable equilibrium ?
Justify your answer in each case.
