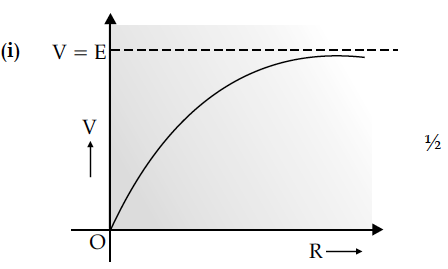
A cell of emf ‘E’ and internal resistance ‘r’ is connected across a variable load resistor R. Draw the plots of the terminal voltage V versus (i) R and
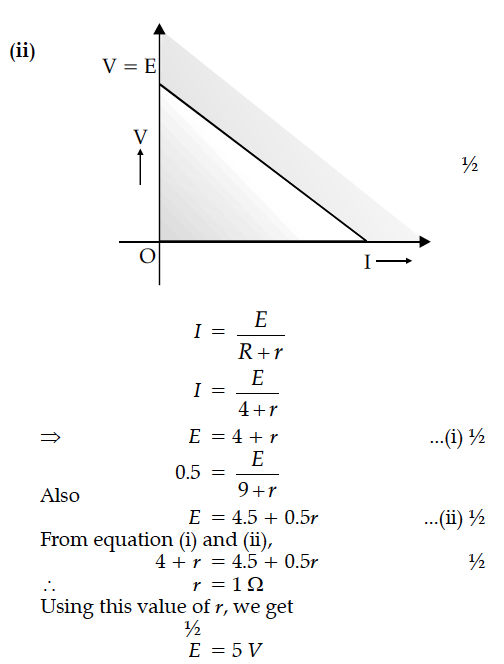
(ii) the current I.
It is found that when R = 4 Ω, the current is 1 A when R is increased to 9 Ω, the current reduces to 0.5 A. Find the values of the emf E and internal resistance r.
(ii) the current I.
It is found that when R = 4 Ω, the current is 1 A when R is increased to 9 Ω, the current reduces to 0.5 A. Find the values of the emf E and internal resistance r.
A battery of emf 10 V and internal resistance 3 ohm is connected to a resistor. If the current in the circuit is 0.5 A, find :
(i) the resistance of the resistor;
(ii) the terminal voltage of the battery.
A battery of emf E and internal resistance, r, when connected with an external resistance of 12Ω produces a current of 0.5 A. When connected across a resistance of 25Ω, it produces a current of 0.25 A. Determine
(i) the emf and (ii) the internal resistance of the cell.
A 9 V battery is connected in series with a resistor. The terminal voltage is found to be 8 V. Current through the circuit is measured as 5 A. What is the internal resistance of the battery?
A cell of emf 4 V and internal resistance 1 W is connected to a d.c. source of 10 V through a resistor of 5 W. Calculate the terminal voltage across the cell during charging.
A 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38Ω as shown in the figure. Find the value of the current in the circuit.
First a set of n equal resistors of R each is connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current becomes 10 times. What is n ?
A battery of emf 12 V and internal resistance 2 Ω is connected to a 4 Ω resistor as shown in the figure.
Define an equipotential surface. Draw equipotential surfaces :
(i) in the case of a single point charge and
(ii) in a constant electric field in z-direction. Why the equipotential surfaces about a single charge are not equidistant ?
(iii) Can electric field exist tangential to an equipotential surface ? Give reason.
(i) Find the value of the phase difference between the current and the voltage in the series LCR circuit shown below. Which one leads in phase : current or voltage ?
(ii) Without making any other change, find the value of the additional capacitor C₁, to be connected in parallel with the capacitor C, in order to make the power factor of the circuit unity.
A 200 mH (pure) inductor and a 5 µF (pure) capacitor are connected one by one, across a sinusoidal ac voltage source of V = [70.7sin (1000t)] voltage. Obtain the expression for the current in each case.
A charge + Q, is uniformly distributed within a sphere of radius R. Find the electric field, due to this charge distribution, at a distant point r from the centre of the sphere where :
(i) 0 < r < R
(ii) r > R
An inductor of 200 mH, capacitor of 400 µF and a resistor of 10 Ω are connected in series to ac source of 50 V of variable frequency. Calculate the
(a) angular frequency at which maximum power dissipation occurs in the circuit and the corresponding value of the effective current, and
(b) value of Q-factor in the circuit.
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity σ of the conductor, when an electric field E, is applied to it.
A source of ac voltage V = V₀ sin ωt, is connected across a pure inductor of inductance L. Derive the expressions for the instantaneous current in the circuit. Show that average power dissipated in the circuit is zero.
