First a set of n equal resistors of R each is connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current becomes 10 times. What is n ?
It is observed that an equivalent resistance of series combination is in series with internal resistance of a battery. Equivalent resistance of parallel combination will also be in series with internal resistance of battery.
Hence in series combination of resistors, current I will be :
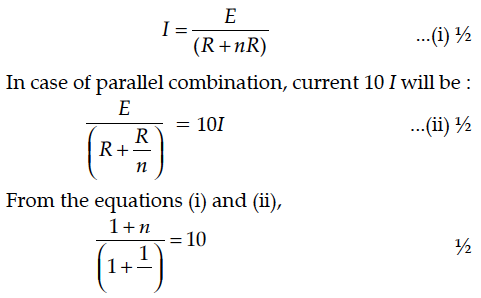
Hence in series combination of resistors, current I will be :
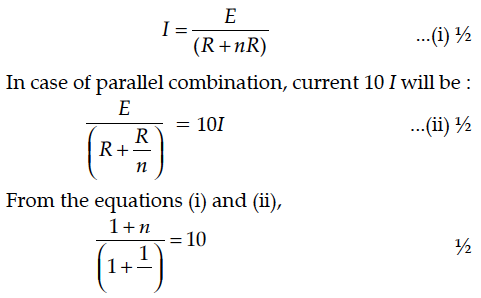
In a Wheatstone bridge, three resistors P,Q, R are connected in three arms in order and 4th arm of resistance, s, is formed by two resistors s1 and s2 connected in parallel. The condition for bridge to be balanced is, P/Q
A network of resistors is connected to a 16 V battery with internal resistance of 1Ω as shown in the Fig. Compute the equivalent resistance of the network.
(a) 5 ohm
(b) 7 ohm
(c) 9 ohm
(d) 10 ohm
A network of resistors is connected to a 16 V battery with internal resistance of 1 Ω, as shown in the following figure. Compute the equivalent resistance of the network.
A 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38Ω as shown in the figure. Find the value of the current in the circuit.
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance ?
Two cells of E.M.F. 10 V and 2 V and internal resistances 10 Ω and 5 Ω respectively, are connected in parallel as shown. Find the effective voltage across R.
A 9 V battery is connected in series with a resistor. The terminal voltage is found to be 8 V. Current through the circuit is measured as 5 A. What is the internal resistance of the battery?
(i) Derive an expression for drift velocity of electrons in a conductor. Hence deduce Ohm’s law.
(ii) A wire whose cross-sectional area is increasing linearly from its one end to the other, is connected across a battery of V volts. Which of the following quantities remain constant in the wire ?
(a) drift speed
(b) current density
(c) electric current
(d) electric field
Justify your answer.
(i) Three point charges q, – 4q and 2q are placed at the vertices of an equilateral triangle ABC of side ‘l’ as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
A voltage V = V₀ sin ωt is applied to a series LCR circuit. Derive the expression for the average power dissipate over a cycle.Under what conditions is
(i) no power dissipated even though the current flows through the circuit,
(ii)maximum power dissipated in the circuit ?
(a) Define the term ‘conductivity’ of a metallic wire. Write its SI unit.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxation time. Hence obtain the relation between current density and the applied electric field E.
An inductor L of inductance is connected in series with a bulb B and an ac source. How would brightness of the bulb change when
(i) number of turns in the inductor is reduced,
(ii) an iron rod is inserted in the inductor and
(iii) a capacitor of reactance is inserted in series in the circuit. Justify your answer in each case.
A sinusoidal voltage of peak value 10 V is applied to a series LCR circuit in which resistance,capacitance and inductance have values of 10 Ω,1 µF and 1 H respectively. Find
(i) the peak voltage across the inductor at resonance
(ii) quality factor of the circuit.
Four point charges Q, q, Q and q are placed at the corners of a square of side ‘a’ as shown in the figure.
