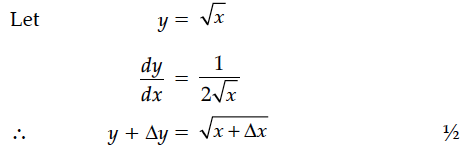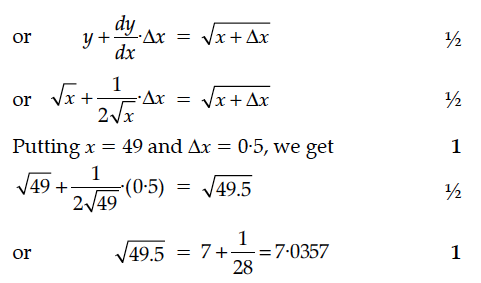Question

Find the general solution of the following differential equation : $y-x{\frac{d y}{d x}}=a\left(y^{2}+{\frac{d y}{d x}}\right).$

Find the point on the curve y = x³ – 11x + 5 at which the equation of tangent is y = x – 11.

If A = $\left(\begin{array}{l l l }1 & -2 & 3 \\ 0 & -1 & 4 \\ -2 & 2 & 1\end{array}\right)$, find $\left(A^{\prime}\right)^{-1}.$

Let A = R – {3}, B = R – {1}. Let f : A → B be defined by f(x) =${\frac{x-2}{x-3}},~~\forall~x\in~A.$ Show that f is bijective. Also, find (i) x, if $f^{-1}(x)$ = 4 (ii) $f^{-1}(7)$

Let f : N → R be a function defined as f(x) = 4x² + 12x + 15. Then show that f : N → S, where S is range of f, is invertible. Also find the inverse of f.

A and B throw a pair of dice alternately. A wins the game if he gets a total of 7 and B wins the game if he gets a total of 10. If A starts the game, then find the probability that B wins.

Show that the equation of normal at any point t on the curve x = 3 cos t – cos³t and y = 3 sin t – sin³t is 4(y cos2t – x sin³t) = 3 sin 4t