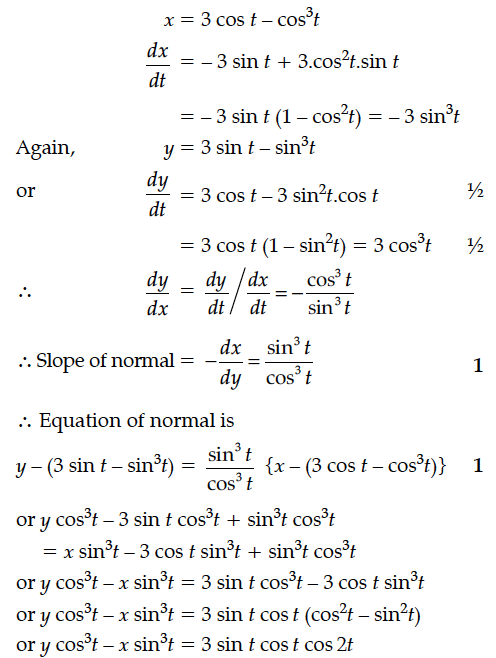
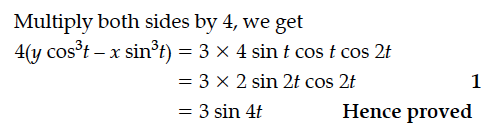
Show that the normal at any point θ to the curve x = a cos θ + aθ sin θ, y = a sin θ – aθ cos θ is at a constant distance from the origin.
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the equation of tangent and normal to the curve x = 1 – cos θ, y = θ – sin θ at θ =
Find the equation of tangent to the curve y = cos (x + y), -2π ≤ x ≤ 0, that is parallel to the line x + 2y = 0.
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Show that the equation of tangent to the parabola y² = 4ax at (x₁, y₁) is yy₁ = 2a(x + x₁).
If Z is the set of all integers and R is the relation on Z defined as R = {(a, b) : a, b ∈ Z and a – b is divisible by 5}. Prove that R is an equivalence relation.
Find the particular solution of the differential equation given that y = 0 when x = 1.
Let f : N → R be a function defined as f(x) = 4x² + 12x + 15. Then show that f : N → S, where S is range of f, is invertible. Also find the inverse of f.
The total cost associated with provision of free mid-day meals to x students of a school in primary classes is given by C(x) = 0·005x³ – 0·02x² + 30x + 50. If the marginal cost is given by rate of change of total cost, write the marginal cost of food for 300 students.