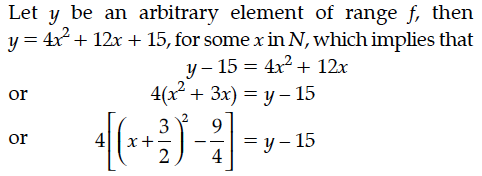
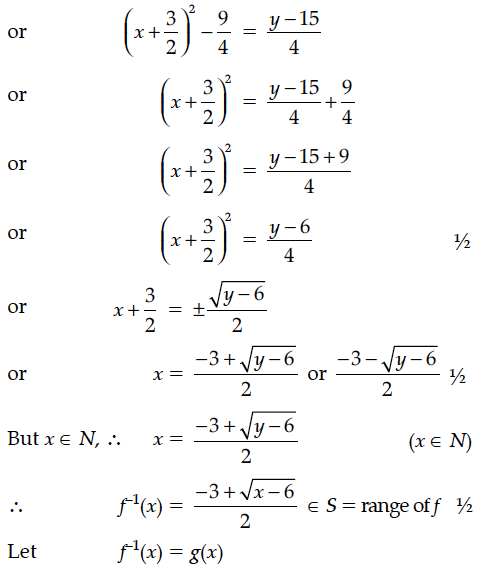
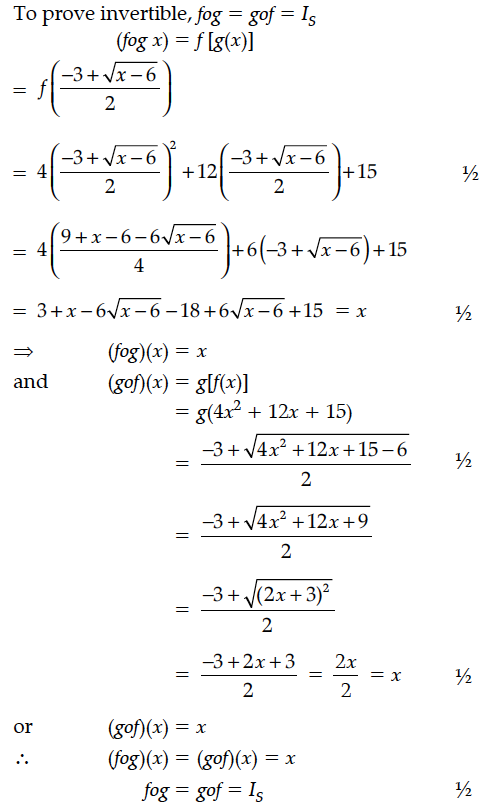
Let f, g : R → R be two functions defined as f (x) = |x| + x and g (x) = |x| – x for all x ∈ R.Then find fog and gof.
Let f : X -> Y be a function. Define a relation R on X given be R = {(a, b) : f(a) = f(b)}. Show that R is an equivalence relation ?
Let f : R → R be defined by f(x) = 3x² – 5 and g : R → R be defined by g(x) = find gof(x) .
If the function f : R → R is given by f(x) = x² + 3x + 1 and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Show that f : N → N, given by f(x) = |``x+1, if x is odd x- 1, if x is even is both one-one and onto.``|
Find the particular solution of the differential equation :
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2 cm/s. How fast is its height on the wall decreasing, when the foot of the ladder is 4 m away from the wall ?
For the curve y = 4x³ – 2x⁵, find all those points at which the tangent passes through the origin.
Find the equation of tangent to the curve y = cos (x + y), -2π ≤ x ≤ 0, that is parallel to the line x + 2y = 0.