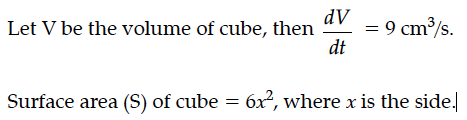
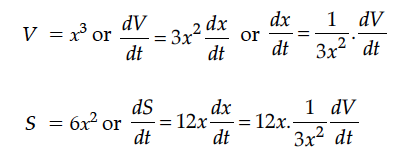
The volume of a sphere is increasing at the rate of 8 cm³/sec. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ?
For the curve y = 5x – 2x³, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3.
Find the slope of tangent to the curve y = 3x² – 6 at the point on it whose x-coordinate is 2.
The equation of tangent at (2, 3) on the curve y² = ax³ + b is y = 4x – 5. Find the values of a and b.
Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.
Find the equations of the normal to the curve y = 4x³ – 3x + 5 which are perpendicular to the line 9x – y + 5 = 0..
A balloon, which always remains spherical, has a variable diameter . Find the rate of change of its volume with respect to x.
The radius r of a right circular cylinder is increasing uniformly at the rate of 0.3 cm/s and its height h is decreasing at the rate of 0.4 cm/s. When r = 3.5 cm and h = 7 cm, find the rate of change of the curved surface area of the cylinder.
If P(E) = 6/11, P(F) = 5/11 and P(E ∪ F) = 7/11 then find
(i) P(E/F)
(ii) P(F/E)
From the differential equation of equation y = a cos 2x + b sin 2x, where a and b are constant.
The radius r of the base of a right circular cone is decreasing at the rate of 2 cm/min. and height h is increasing at the rate of 3 cm/min. When r = 3.5 cm and h = 6 cm, find the rate of change of the volume of the cone.
Three cards are drawn without replacement from a pack of 52 cards. Find the probability that
(i) the cards drawn are king, queen and jack respectively.
(ii) the cards drawn are king, queen and jack.