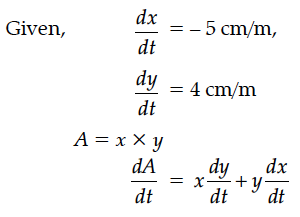
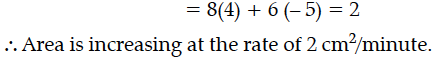
The radius r of a right circular cone is decreasing at the rate of 3 cm/minute and the height h is increasing at the rate of 2 cm/minute. When r = 9 cm and h = 6 cm, find the rate of change of its volume.
The radius r of a right circular cylinder is increasing at the rate of 5 cm/min and its height h, is decreasing at the rate of 4 cm/min. When r= 8 cm and h = 6 cm, find the rate of change of the volume of cylinder.
The radius r of a right circular cylinder is decreasing at the rate of 3 cm/min. and its height h is increasing at the rate of 2 cm/min. When r =7 cm and h = 2 cm, find the rate of change of the volume of cylinder.
The radius r of the base of a right circular cone is decreasing at the rate of 2 cm/min. and height h is increasing at the rate of 3 cm/min. When r = 3.5 cm and h = 6 cm, find the rate of change of the volume of the cone.
The volume of a sphere is increasing at the rate of 8 cm³/sec. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ?
The volume of a cube is increasing at the rate of 9 cm³/sec. How fast is the surface area increasing when the length of an edge is 10 cm.
Find the area of the parallelogram whose diagonals are represented by the vectors = and
A balloon, which always remains spherical, has a variable diameter . Find the rate of change of its volume with respect to x.
A particle moves along the curve 6y = x³ + 2. Find the points on the curve at which y-coordinate is changing 2 times as fast as x-coordinate.
If P(F) = 0·35 and P(E U F) = 0·85 and E and F are independent events. Find P(E).
If P(A) = 0.4, P(B) = p, P(A U B) = 0.6 and A and B are given to the independent events, find the value of ‘p’.