For the curve y = 5x – 2x³, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3.
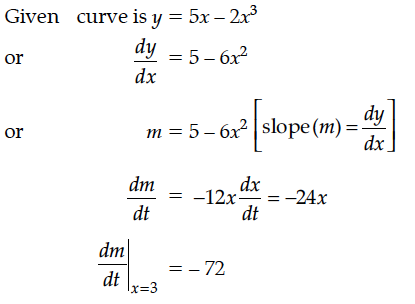
Rate of Change of the slope is decreasing by 72
units/s.
For the curve y = 4x³ – 2x⁵, find all those points at which the tangent passes through the origin.
The volume of a cube is increasing at the rate of 9 cm³/sec. How fast is the surface area increasing when the length of an edge is 10 cm.
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing when the side of the triangle is 20 cm ?
Find the equations of the normal to the curve y = x³+ 2x + 6, which are parallel to line x + 14y + 4 = 0.
If the radius of sphere is measured as 9 cm with an error of 0.03 cm, then find the approximate error in calculating its surface area.
The volume of a sphere is increasing at the rate of 8 cm³/sec. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm.
If A and B are two independent events, prove that A’ and B are also independent.
For the curve y = 5x – 2x³, if x increases at the rate of 2 units/sec, then find the rate of change of the slope of the curve when x = 3.
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy
(ii) the older child is a boy.
Find the inverse of the matrix Hence, find the matrix P satisfying the matrix equation P = .
How many equivalence relations on the set {1, 2, 3} containing (1, 2) and (2, 1) are there in all ?Justify your answer.
