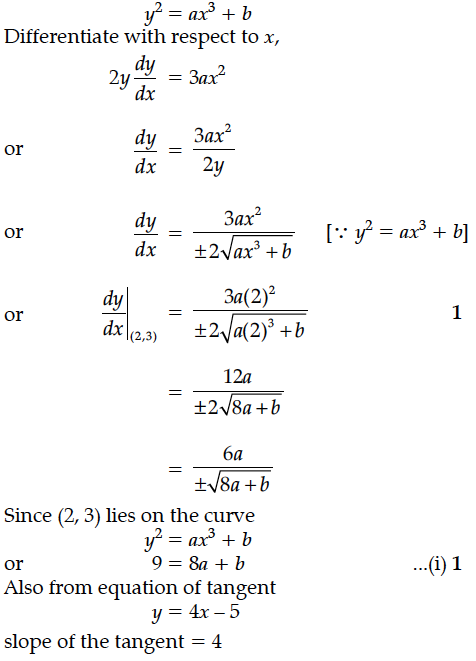
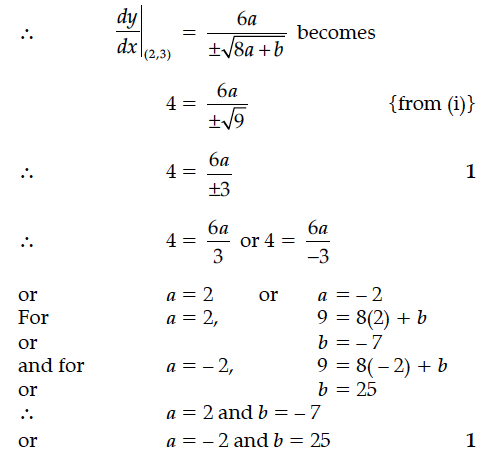
Find the equation of tangent to the curve 4x² + 9y² = 36 at the point (3 cos θ, 2 sin ).
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Find the equation of the tangent to the curve y = x⁴ – 6x³ + 13x² – 10x + 5 at point x = 1, y = 0.
Find the equations of the normal to the curve x² = 4y which passes through the point (1, 2).
Find the slope of tangent to the curve y = 3x² – 6 at the point on it whose x-coordinate is 2.
Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.
Find the equations of the tangent and normal to the curve x = a sin³θ, y = b cos³θ at
Find the equation of tangents to the curve y = x³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0.
In a school, there are 1,000 students, out of which 380 are girls. Out of 380 girls, 10% of the girls scored highest in GS. What is the probability that a student chosen randomly scored highest in GS given that the chosen student is a girl ?
Let A = {1, 2, 3, . ...., 9} and R be the relation in A × A defined by (a, b) R (c, d) if a + d =b + c for (a, b), (c, d) in A × A. Prove that R is an equivalence relation. Also obtain the equivalence class [(2, 5)].
If the function f : R → R is given by f(x) = and g : R → R is given by g(x) = 2x – 3, then find
(i) fog (ii) gof
Is f⁻¹ = g?
The amount of pollution content added in air in a city due to x-diesel vehicles is given by p(x) = 0·005x³ + 0·02x² + 30x. Find the marginal increase in pollution content when 3 diesel vehicles are added.
A problem in mathematics is given to 4 students A, B, C, D. Their chances of solving the problem, respectively, are 1/3, 1/4, 1/5 and 2/3. What is the probability that
(i) the problem will be solved ?
(ii) at most one of them solve the problem ?