Three cards are drawn without replacement from a pack of 52 cards. Find the probability that
(i) the cards drawn are king, queen and jack respectively.
(ii) the cards drawn are king, queen and jack.
(i) the cards drawn are king, queen and jack respectively.
(ii) the cards drawn are king, queen and jack.
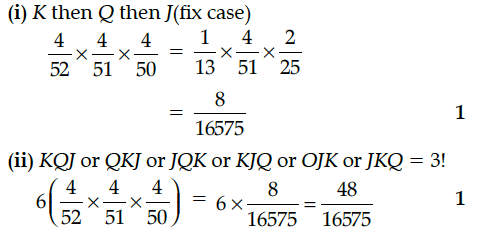
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy
(ii) the older child is a boy.
If E and F are independent events, then show that
(i) E and F' are independent events.
(ii) E' and F are also independent events.
If A and B are two independent events, then prove that the probability of occurrence of at least one of A and B is given by 1 – P(A’) · P(B’)
P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree
in stating the same fact ?
A and B throw a pair of dice alternatively, till one of them gets a total of 10 and wins the game. Find their respective probabilities of winning, if A starts first.
If E and F be two events such that P(E) = 1/3, P(F) = 1/4, find P(E U F) if E and F are independent events.
If A and B are two independent events such that P(A' ∩ B)= 2/15 and P(A ∩ B')= 1/6, then find P(A) and P(B).
The radius r of the base of a right circular cone is decreasing at the rate of 2 cm/min. and height h is increasing at the rate of 3 cm/min. When r = 3.5 cm and h = 6 cm, find the rate of change of the volume of the cone.
Show that the function f given by f(x) = tan⁻¹ (sin x+ cos x) is decreasing for all
If E and F are two events such that P(E) = 1/4, P(F) = 1/2 and P(E ∩ F) = 1/8, find
(i) P(E or F)
(ii) P(not E and not F).
If E and F are independent events, then show that
(i) E and F' are independent events.
(ii) E' and F are also independent events.
