Find the particular solution of the differential equation given that y = 0 when x = 1.
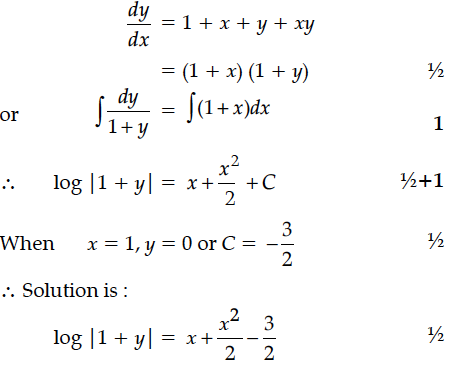
Find the particular solution of the differential equation given that y = 0, when x = 0.
Find the particular solution of the differential equation given that x = 0 when y = 1.
Find the particular solution of the differential equation (x – sin y) dy + (tan y) dx = 0, given that y = 0 when x = 0.
Find the particular solution of the differential equation given that y = 1, when x = 0.
Find the particular solution of differential equation : given that y = 1 when x = 0.
Find the particular solution of the following differential equation :
given that y = 1, when x = 0.
Find the particular solution of the differential equation x (1 + y²) dx – y (1 + x²) dy = 0, given that y = 1, when x =0.
Find the equation of tangent to the curve x² + 3y = 3, which is parallel to line y – 4x + 5 = 0.
Let A = {1, 2, 3, . ...., 9} and R be the relation in A × A defined by (a, b) R (c, d) if a + d =b + c for (a, b), (c, d) in A × A. Prove that R is an equivalence relation. Also obtain the equivalence class [(2, 5)].
Find the particular solution of the differential equation given that y = 0 when x = 1.
Let f : N → R be a function defined as f(x) = 4x² + 12x + 15. Then show that f : N → S, where S is range of f, is invertible. Also find the inverse of f.
