Question

Solve the following differential equation : ${\frac{d y}{d x}}\ +\,\sec x{y}=\tan x,\left(0\leq x<{\frac{\pi}{2}}\right)\!.$

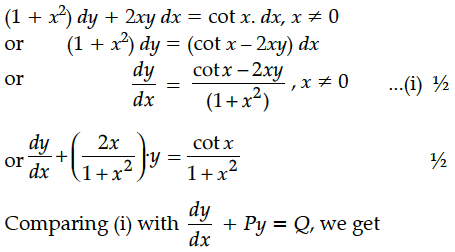
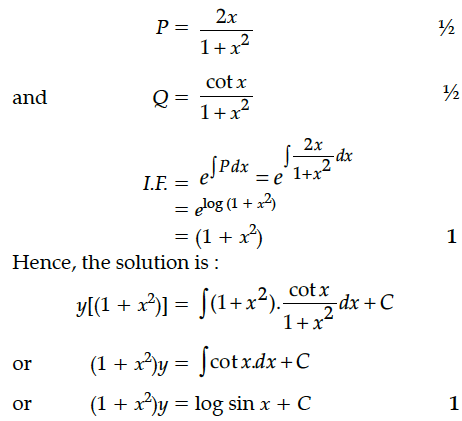
A trust fund has ₹ 35,000 is to be invested in two different types of bonds. The first bond pays 8% interest per annum which will be given to orphanage and second bond pays 10% interest per annum which will be given to an N.G.O. (Cancer Aid Society). Use matrix multiplication, determine how to divide ₹ 35,000 among two types of bonds if the trust fund obtains an annual total interest of ₹ 3,200.

In a parliament election, a political party hired a public relations firm to promote its candidates in three ways — telephone, house calls and letters. The cost per contact (in paise) is given in matrix A as

Evaluate : ($\large\textstyle\int(3x-2){\sqrt{x^{2}+x+1}}\,d x~.$

If Z is the set of all integers and R is the relation on Z defined as R = {(a, b) : a, b ∈ Z and a – b is divisible by 5}. Prove that R is an equivalence relation.

Find : $\large\textstyle\int$$(x+3){\sqrt{3-4x-x^{2}}}\ d x\ .$

Find the particular solution of the following differential equation : ${\frac{d y}{d x}}\;=1+x^{2}+y^{2}+x^{2}y^{2},$ given that y = 1, when x = 0.